Working around, I found some Tan Binomial formulas.
Let's $S$ be a set such that:
$$ S=\left\{\text{ }\tan ^2\left(\frac{1\pi }{n}\right), \tan^2\left(\frac{2\pi }{n}\right), \tan^2\left(\frac{3\pi }{n}\right)\text{ },\text{...},\tan^2\left(\frac{k \pi }{n}\right) \right\} \text{for } k \text{ in } \text{range } \left[ 1,\left\lfloor \frac{(n-1)}{2}\right\rfloor \right] $$
and let's $S_k$ be a k-subset of $S$. For example, for k=2, we have:
$$ S_k = \left\{\text{ }\left\{\tan ^2\left(\frac{1\pi }{n}\right), \tan ^2\left(\frac{2\pi }{n}\right)\right\},\left\{\tan ^2\left(\frac{1\pi }{n}\right), \tan ^2\left(\frac{3\pi }{n}\right)\right\},\text{...} ,\left\{\tan ^2\left(\frac{(k-1)\pi }{n}\right), \tan ^2\left(\frac{k \pi }{n}\right)\right\}\right\} $$
Then one formula gives:
$$ \left\{ \begin{array}{c} \text{if n Even},\text{ }n\times \left(\text{Sum of the Product of k-Subset }S_k\right)=\left( \begin{array}{c} n \\ 2k+1 \end{array} \right) \\ \text{if n Odd},\text{ }\left( \text{Sum of the Product of k-Subset } S_k \right)=\left( \begin{array}{c} n \\ 2k \end{array} \right) \end{array} \right. $$
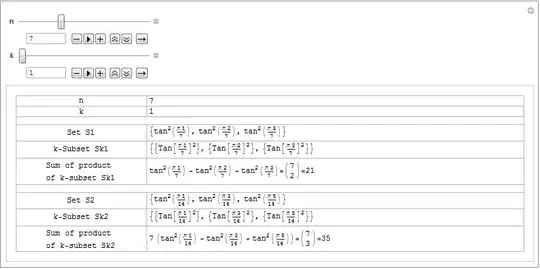
Here are some examples with n=7 and k varying from 1 to 3. We have: $S=\left\{\tan ^2\left(\frac{\pi 1}{7}\right),\tan ^2\left(\frac{\pi 2}{7}\right),\tan ^2\left(\frac{\pi 3}{7}\right)\right\}$
- for k=1, k-subset is $S_1=\left\{ \left\{\tan ^2\left(\frac{\pi 1}{7}\right)\right\},\left\{\tan ^2\left(\frac{\pi 2}{7}\right)\right\},\left\{\tan ^2\left(\frac{\pi 3}{7}\right)\right\} \right\}$, so $\tan ^2\left(\frac{\pi 1}{7}\right)+\tan ^2\left(\frac{\pi 2}{7}\right)+\tan ^2\left(\frac{\pi 3}{7}\right)=\left( \begin{array}{c} 7 \\ 2 \end{array} \right)=21$
- for k=2, k-subset is $S_2=\left\{ \left\{\tan ^2\left(\frac{\pi 1}{7}\right),\tan ^2\left(\frac{\pi 2}{7}\right)\right\},\left\{\tan ^2\left(\frac{\pi 2}{7}\right),t\tan ^2\left(\frac{\pi 3}{7}\right)\right\},\left\{\tan ^2\left(\frac{\pi 1}{7}\right),t\tan ^2\left(\frac{\pi 3}{7}\right)\right\} \right\}$, so $\tan ^2\left(\frac{\pi 1}{7}\right) \tan ^2\left(\frac{\pi 2}{7}\right)+\tan ^2\left(\frac{\pi 3}{7}\right) \tan ^2\left(\frac{\pi 2}{7}\right)+\tan ^2\left(\frac{\pi 1}{7}\right) \tan ^2\left(\frac{\pi 3}{7}\right)=\left( \begin{array}{c} 7 \\ 4 \end{array} \right)=35$
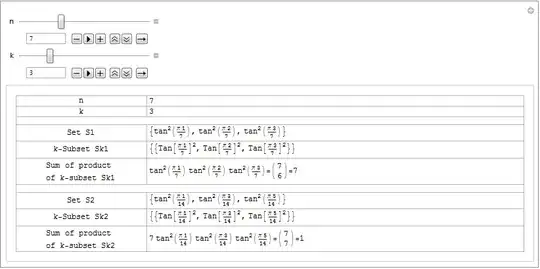
- for k=3, k-subset is $S_3=\left\{ \left\{\tan ^2\left(\frac{\pi 1}{7}\right),\tan ^2\left(\frac{\pi 2}{7}\right),\tan ^2\left(\frac{\pi 3}{7}\right)\right\} \right\}$, so $\tan ^2\left(\frac{\pi 1}{7}\right) \tan ^2\left(\frac{\pi 2}{7}\right) \tan ^2\left(\frac{\pi 3}{7}\right)=\left( \begin{array}{c} 7 \\ 6 \end{array} \right)=7$

Here is the Mathematica code corresponding to the images, if someone wants to play around:
Manipulate[
Module[
{
set1,S1,Sk1,psk1,pskEven1,
set2,S2,Sk2,psk2,pskEven2,
ProdSumSubset,binEven,bin1,bin2,
hf,rh,opt1
},
hf[x_]:=HoldForm@x;
rh[x_]:=ReleaseHold@x;
set1[n_]:=Table[ Tan[hf@( k)*Pi/hf@(n) ]^2,{k,1,Floor@((n-1)/2)}] ;
set2[n_]:=Table[ Tan[hf@(2 k-1)*Pi/hf@(2*n) ]^2,{k,1,Floor@(n/2)}] ;
ProdSumSubset[S_,k_]:=Plus@@(Times@@#&/@ Subsets[S,{k}]);
bin1[n_,k_]:=Binomial[n,hf@(2*k)];
bin2[n_,k_]:=Binomial[n,hf@(2*k+1)];
opt1={ Frame->All,Alignment->{{Center,Left},Center},ItemSize->{{[email protected],[email protected]}},FrameStyle->GrayLevel[0.7`] };
TraditionalForm@
Grid[
{
{ "n",n },
{ "k",k },
{"",SpanFromLeft},
{ "Set S1",S1=set1[n] },
{ "k-Subset Sk1",Sk1=Subsets[S1,{k}]//StandardForm },
psk1=ProdSumSubset[S1,k];
pskEven1=If[ EvenQ@n,n*psk1,psk1 ];
binEven=If[ EvenQ@n,bin2[n,k],bin1[n,k] ];
{ "Sum of product of k-subset Sk1",Row[{ pskEven1,"=", pskEven1//rh//N,"=",binEven,"=",binEven//rh}] },
{"",SpanFromLeft},
{ "Set S2",S2=set2[n] },
{ "k-Subset Sk2",Sk2=Subsets[S2,{k}]//StandardForm },
psk2=ProdSumSubset[S2,k];
pskEven2=If[ EvenQ@n,psk2,n*psk2 ];
binEven=If[ EvenQ@n,bin1[n,k],bin2[n,k] ];
{ "Sum of product of k-subset Sk2",Row[{ pskEven2,"=", pskEven2//rh//N,"=",binEven,"=",binEven//rh}] }
},opt1
]
]
,{{n,7},1,20,1,Appearance->"Open"}
,{{k,1},1,10,1,Appearance->"Open"}
]
The same holds for a set $S$ such that:
$$ S=\left\{\text{ }\tan ^2\left(\frac{1\pi }{2n}\right), \tan ^2\left(\frac{3\pi }{2n}\right), \tan ^2\left(\frac{5\pi }{2n}\right)\text{ },\text{...},\tan ^2\left(\frac{(2k-1)\pi }{2n}\right) \right\} \text{for}\text{ }k\text{ }\text{in}\text{ }\text{range} \left[ 1,\left\lfloor \frac{n}{2}\right\rfloor \right] $$
then:
$$ \left\{ \begin{array}{c} \text{if } n \text{ Even}, \left( \text{Sum } \text{of } \text{the } \text{Product } \text{of } k-\text{Subset }S_k \right)=\left( \begin{array}{c} n \\ 2k \end{array} \right) \\ \text{if } n \text{ Odd},\text{ }n\times \left( \text{Sum } \text{of } \text{the } \text{Product } \text{of } k-\text{Subset } S_k \right)=\left( \begin{array}{c} n \\ 2k+1 \end{array} \right) \end{array} \right. $$
For example, for n=6 and k=2: $$ \tan ^2\left(\frac{\pi 1}{12}\right) \tan ^2\left(\frac{\pi 3}{12}\right)+\tan ^2\left(\frac{\pi 1}{12}\right) \tan ^2\left(\frac{\pi 5}{12}\right)+\tan ^2\left(\frac{\pi 3}{12}\right) \tan ^2\left(\frac{\pi 5}{12}\right)=\left( \begin{array}{c} 6 \\ 4 \end{array} \right)=15 $$
$ $
$ $
These formulas can be explained this way:
Let's
$z=1+i x=|z|e^{i \text{arcTan}(x)}$ and it's complex conjuguate
$z^*=1-i x=|z|e^{-i \text{arcTan}(x)}$
then:
$$
\text{Cos}(n \text{Arctan} x)=\frac{z^n+z^{*n}}{2 |z|^n}=\frac{(1+i x)^n+(1-i x)^n}{2\left(1+x^2\right)^{\frac{n}{2}}}=\frac{\sum _{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor } (-1)^k\text{ }\left(
\begin{array}{c} n\\2 k\end{array}
\right)x^{2 k}}{\left(1+x^2\right)^{\frac{n}{2}}}
$$
Where the numerator is a binomial polynomial (For ex:$\text{Cos} (6 \text{Arctan} x)=\frac{-x^6+15 x^4-15 x^2+1}{\left(x^2+1\right)^3}$,$\text{Cos} (7 \text{Arctan} x)=\frac{-7 x^6+35 x^4-21 x^2+1}{\left(x^2+1\right)^{7/2}}$,etc...) admitting solutions in the form $\pm \text{Tan}\left(\frac{(2k+1) \pi }{2n}\right)$ for $k\in\mathbb{N}$.
Using a set $S=\left\{\text{ }\tan ^2\left(\frac{1\pi }{2n}\right), \tan ^2\left(\frac{3\pi }{2n}\right), \tan ^2\left(\frac{5\pi }{2n}\right)\text{ },\text{...},\tan ^2\left(\frac{(2k-1)\pi }{2n}\right) \right\}$ with $k$ in range $\left[1,\left\lfloor\frac{n}{2}\right\rfloor\right]$, we can then rewrite the numerator as a same order polynomial:
$$
\text{Cos}(n \text{Arctan} x)=\frac{\left(x^2-\text{Tan}^2\left(\frac{1\pi }{2n}\right)\right)\left(x^2-\text{Tan}^2\left(\frac{3\pi }{2n}\right)\right)\text{...}\left(x^2-\text{Tan}^2\left(\frac{(2k-1)\pi }{2n}\right)\right)}{\left(1+x^2\right)^{\frac{n}{2}}}
$$
Expanding the numerator and matching the binomial coefficient for each order gives one formula, the other coming from:
$$
\text{Sin}(n \text{Arctan} x)=\frac{z^n-z^{*n}}{2i |z|^n}=\frac{\sum _{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor } (-1)^k\text{ }\left(
\begin{array}{c}
n \\
2 k+1
\end{array}
\right)x^{2 k+1}}{\left(1+x^2\right)^{\frac{n}{2}}}
$$
And using the same reasoning.
$ $
$ $
I could not find these formulas on the web, only special cases. Could someone tell me if they exist?
$z=1+i x=|z|e^{i \text{arcTan}(x)}$ and
$z^=1-i x=|z|e^{-i \text{arcTan}(x)}$
then for Cos:
$ \text{Cos} (n \text{Arctan} x)=\frac{z^n+z^{n}}{2 |z|^n} = \frac{(1+i x)^n+(1-i x)^n}{2\left(1+x^2\right)^{\frac{n}{2}}} $
where the numerator is $ \sum _{k=0}^{\left\lfloor \frac{n}{2}\right\rfloor } (-1)^k\left( \begin{array}{c} n \ 2k \end{array} \right)x^{2k} $ – Eddy Khemiri Oct 13 '13 at 18:22
$ \left(x^2-\text{Tan}^2\left(\frac{1\pi }{n}\right)\right)\left(x^2-\text{Tan}^2\left(\frac{2\pi }{n}\right)\right)\text{...}\left(x^2-\text{Tan}^2\left(\frac{\text{k$\pi $}}{n}\right)\right) $
expanding and matching the binomial coefficients, you get the formulae.
And same thing for $ \text{Sin} (n \text{Arctan} x) $. – Eddy Khemiri Oct 13 '13 at 18:23