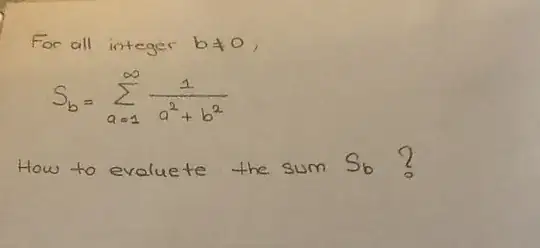This question is from my notebook, not hw or else, only exercise to understand better. I tried by myself. However, since my trail are too trivial, I dont need to write here. i am confused a bit. I want to learn how to solve such question types. I guess I need to use residue. I am grateful to help me thank you.
we'll use the integral $$ \oint_{C_N} \frac{\pi\cot(\pi z)}{z^2 + b^2 } \ dz $$
where $C_N $ is the square contour of side $ 2N + 1 $
By residues theory :
$$ \oint_{C_N} \frac{\pi\cot(\pi z)}{z^2 + b^2 } \ dz = 2\pi i\left( \sum_{-N}^N \mathrm{Res} \left( \frac{\pi\cot(\pi z)}{z^2 + b^2 } , n \right) + \mathrm{Res} \left( \frac{\pi\cot(\pi z)}{z^2 + b^2 } , bi \right) + \mathrm{Res} \left( \frac{\pi\cot(\pi z)}{z^2 + b^2 } , -bi \right) \right)$$
the integral $ \to 0 $ as $ N \to \infty $
$$ \Rightarrow \sum_{-\infty }^{\infty} \mathrm{Res} \left( \frac{\pi\cot(\pi z)}{z^2 + b^2 } , n \right) + \mathrm{Res} \left( \frac{\pi\cot(\pi z)}{z^2 + b^2 } , bi \right) + \mathrm{Res} \left( \frac{\pi\cot(\pi z)}{z^2 + b^2 } , -bi \right) = 0 $$
$$ \Rightarrow \sum_{-\infty}^{-1} \frac{1}{n^2 + b^2} + \sum_{1}^{\infty} \frac{1}{n^2 + b^2 } + \frac{1}{b^2} + \lim_{z \to bi} \frac{\pi\cot(\pi z)}{z + bi} + \lim_{z \to -bi} \frac{\pi\cot(\pi z)}{z - bi} = 0$$
$$ \Rightarrow 2\sum_{n=1}^{\infty} \frac{1}{n^2 + b^2 } + \frac{1}{b^2} - \frac{\pi\coth(b\pi)}{b} = 0 $$
$$ \Rightarrow \sum_{n=1}^{\infty} \frac{1}{n^2 + b^2 } = \frac{\pi\coth(b\pi)}{2b} - \frac{1}{2b^2} $$
