Just out of curiosity, since $$\sum_{i>0}\frac{9\times10^{i-1}}{10^i}, \quad\text{ or }\quad 0.999\ldots=1,$$ Does that mean $0.999\ldots=1$, or in other words, that $0.999\ldots$ is an integer, by applying the transitive property?
Ty.
Asked
Active
Viewed 1,084 times
2
-
8"…since $0.999\ldots=1$, does that mean $0.999\ldots=1$…?" Yes. It seems you've answered your own question. – Sep 25 '13 at 02:17
-
1 is an integer, and $\overline{.9}=1$, so $\overline{.9}$ is an integer. – tylerc0816 Sep 25 '13 at 02:17
-
For explanation why it is 1, I think this question was answered in great detail not so long ago. Does anyone remember?? – imranfat Sep 25 '13 at 02:18
-
@imranfat Here's that question: http://math.stackexchange.com/questions/11/does-99999-1/ – Chris Culter Sep 25 '13 at 02:27
-
Only if you assume that whenever a is true and b is true that a&b is true, for any statements a, b. – Loki Clock Sep 25 '13 at 03:29
-
$\Huge YES$. It's true. – Felix Marin Sep 25 '13 at 03:30
-
Your question should have been: "if $a=b$ and $b=c$, does $a=c$?" – Cheerful Parsnip Nov 22 '13 at 20:55
-
http://math.stackexchange.com/questions/104530/how-do-we-prove-that-lfloor0-999-cdots-rfloor-lfloor-1-rfloor – jimjim Nov 22 '13 at 21:30
3 Answers
14
$0.999999\ldots$ is indeed $1$, which indeed is a natural number and therefore an integer.
-
@CommanderShepard: But wait, natural numbers do not have fractional parts, how is that justified? – jimjim Nov 22 '13 at 21:35
-
2
-
@PedroAmaralCouto : excellent point, I don't know . I am giving up on these types of questions, can't even think if it should or shouldn't be a natural number. – jimjim Jul 31 '22 at 13:40
1
For all $a \in \mathbb{R}$ if there is a sequence that gets arbitrarily close in the sense that all neighborhoods around the point contain all $a_n$ such that $n \gt N$ for some $N$ natural depending on the neighborhood, the the sequence is said to converge to a point. $0.999\dots$ is defined to be the limit of such a sequence and the limit happens to be $1$ mysteriously.
The sequence is you guessed it! $0.9, \ 0.99, \ 0.999, \ \dots$ Prove that this sequence $\{a_n\}$ converges to $1$ by showing that for all $\epsilon \gt 0 \in \mathbb{R}$ there exists $N \in \mathbb{N}$ such that for all $n\gt N$, $ \ |1 - a_n|\lt \epsilon$. Then you can say that $\lim a_n = 1$ by definition.
Daniel Donnelly
- 21,342
1
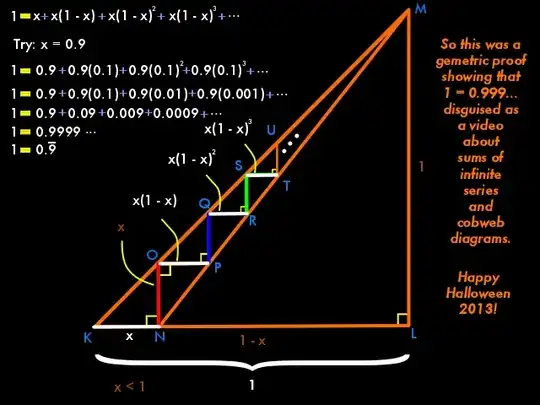
It is an integer and the integer is 1. I recently made a Halloween video on cobweb diagrams with a visual proof of this result (which is meant to be a surprise, but I'm spoiling it, sorry). With the cobweb diagram and a knowledge of geometry, you can visualize why 1 is the infinite sum. The two notations 1 and 0.9999... represent the exact same length, the integer 1. The proof is my own which was modified from a visual proof on infinite series (see part 1 of the videos).
Here is video of my proof explained: http://www.youtube.com/watch?v=MhaRGt9rmyo
And if I'm lucky this one image will convey the whole proof (The length of the bottom of the triangle is 1 which is the same as the sum of all the white horizontal lengths, reaching up to infinity at point M, 0.9 + 0.09 + 0.009 + ...). Obviously x is not drawn to scale with 1, but this is done to show the "cobweb" better. The video walks through the geometric proof.
