5

Can anyone explain branch points, cuts, branches, and Riemann surfaces on this example: $$ f(z)=\sqrt {z-4} + \sqrt[4]{z} $$

Bojana
  • 53

4 Answers4

7

The question seems to have been edited... I saw the query about $\sqrt{z}+(z-2)^{1/3}$. I'll do the revised version afterward. The branch points are where either of the two radicals behaves strangely (has fewer than the expected number of distinct roots), namely, 0 and 2.

Over every point other than 0, there are two branches of the square root. To make two single-valued square roots, "cutting" the plane along any ray from 0 to infinity works.

Over everypoint other than 2, there are three branches of that cube root. To make three single-valued cube roots, cut the plane along any ray from 2 to infinity.

To take care of both radicals simultaneously, basically we need two rays, one from 0 to infinity, the other from 2 to infinity. We could take a ray that starts at 0, passes through 2, and goes to infinity, but this is a slightly weird choice, and doesn't really help anything much.

The Riemann surface has to be/is a "ramified covering" of the plane on which the function is well-defined. This requires a six-sheeted covering to incorporate the $2\cdot 3$ sheets needed by the square root and the cube root.

To determine the genus via the Riemann-Hurwitz formula, observe that the point at infinity has six-fold ramification, giving one point with ramification degree 6. There are 3 different points with ramification degree 2, and 2 points with ramification degree 3. Thus, by Riemann-Hurwitz, $$ 2 - 2g' = 6(2 - 2g) - \sum_P (e_P-1) = 12 - ((6-1)+3(2-1)+2(3-1)) = 12 - 12$$ Thus, the genus of the cover is $g'=1$. [Edited: garbled Riemann-Hurwitz!]

With $\sqrt{z}+(z-4)^{1/4}$, there are 8 sheets altogether. The point at infinity behaves a little differently, since the cover on which $(z-4)^{1/4}$ exists near infinity already has a $\sqrt{z}$ there. Thus, there are two points lying over the point at infinity, each with ramification degree 4. There are 4 points lying over 0, each with ramification 2, and 2 points over 4, each of ramification 4. Riemann-Hurwitz is $$ 2-2g' = 8(2 - 2g) - \sum_P(e_P-1) = 16 - (2(4-1)+4(2-1)+2(4-1)) = 16 - 16$$ so the genus of the cover is $g'=1$.

paul garrett
  • 52,465
  • 1
    you forgot a little thing in the Riemann-Hurwitz formula: it's rather $2-2g'=n(2-2g)-\sum_P(e_p-1)$, where $n$ is the number of sheets (in this case $n=6$, hence $g'=1$ (I hope)) – user8268 Jul 08 '11 at 19:18
  • Sorry for the edit, I thought nobody was trying to answer me so there would be no damage to change the function to one I actually need. Thanks for your effort and for Riemann-Hurwitz formula, I'm now going to check out rest of your answer. Cheers – Bojana Jul 08 '11 at 19:20
  • Ooops, yes, you're right, sorry! Fixed it above... Wouldn't want to mislead anyone! – paul garrett Jul 08 '11 at 19:25
  • Also I need to determine branches explicitly if that's not a problem. Thanks – Bojana Jul 08 '11 at 19:34
  • The branches will correspond to the $2\times 4$ branches of square-root $\times$ fourth-root. That is, over a non-ramified point, you just list those 8 possibilities with the sign-flip on sqrt and $\pm 1,\pm i$ on the fourth root. – paul garrett Jul 08 '11 at 19:46
  • ... and, paying attention to particulars, one could anticipate how the computation of genus would turn out: in stages, taking a square root gives a genus-zero surface. Taking a fourth root of a quartic over a genus-zero surface gives an elliptic curve (genus 1). Similarly with the earlier version: the quadratic extension leaves the genus at 0, and a square-root-of-cubic gives genus 1. – paul garrett Jul 08 '11 at 21:40
  • Bojana: you just need to draw a curve(s) C(t) passing through/contaiining the branch points; that way no curve in the remaining $\mathbb C$-{C(t)} can wind around a branch point; that allows your function to be well-defined. – gary Jul 09 '11 at 14:34
  • (Cont.) Maybe it is more clear to say that you need to remove C(t) , so that after removing, no curves will wind around branch points. – gary Jul 09 '11 at 14:44
  • A late comment: how do you find ramification points of $f(z)=\sqrt{z}+(z-2)^{\frac 13}$ and their ramification degree? I tried to find zero of $f'(z)=0$, but that doesn't work. – Andrews Jun 10 '19 at 07:27
3

As a way of visualizing the Riemann surface of $\sqrt{z-4} + \sqrt[4]z$, let's look at the real and imaginary components:

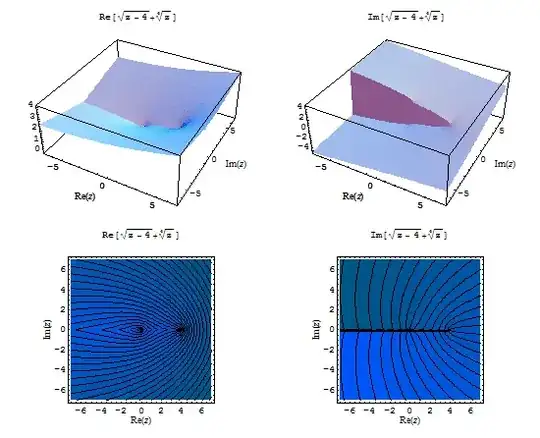
Riemann surface

The branch points $z=0$ and $z=$ are noticeable in the plots of the real part, while the cuts can be seen in the plots of the imaginary part.

J. M. ain't a mathematician
  • 75,051
  • I did this with an old version of Mathematica; maybe somebody with $VersionNumber > 5 could make a better version of these pictures. Feel free to edit if you've better pics... – J. M. ain't a mathematician Jul 16 '11 at 08:32
1

if you want some general intuition, first you can see that the cover is eight-sheeted (as there are two times four possible values for the function). the "bad" points are 0 and 4. fix some point on the cover, say near a point over zero (i.e. pick a branch of the square root and the fourth root). if you loop around this point four times, you come back to the same value (the square root isn't changing, just the fourth root). there will be another point over zero (corresponding to the other choice of square root) that you can loop around four times. so there are two ramified points over zero (each one corresponding to a choice of square root). similarly, there are four ramified points over 4 which you can go around twice.

if you have some time on your hands, get eight pieces of paper, put two dots (for 0 and 4) on the same place on each, make two cuts on each piece in the same place radiating out from the two dots.

take a stack of four and say this is the + square root, then tape the four sheets in a spiral around "zero". take the other stack of four (the - square root) and do the same. (you wont be able to get the 4-periodicity but oh well.)

now you have to align the + and - square roots, which is just about impossible (you might get one of the four pairs and then still without the 2-periodicity).

anyway, it gives you a rough idea of what the thing looks like...

yoyo
  • 9,943
0

To clarify what happens at infinity, at each point $(z,f(z))$, you have enough information to know the values of $g(z) = \sqrt{z}$ and $h(z) = \sqrt[4]{z-2}$ ($g$ and $h$ can be expressed as polynomials in $f$ but they're ugly).

So at each point you can attach the value of $g/h^2$. As $z$ goes to infinity, you have that $g^2/h^4 = z/(z-2)$ converges to $1$, so $g/h^2$ must converge to $1$ or $-1$.

The two points over infinity make precisely this distinction. There is one point on which $g/h^2$ is $1$, the other on which $g/h^2$ is $-1$. Each time you loop around infinity, $g$ gets multiplied by $-1$, and $h$ gets multiplied by $\pm i$ (it depends on the way you are making your loop). So after 4 loops, you end up on your starting point, so each point has 4 branches. Since there are 8 branches, these can be the only two points.

mercio
  • 50,180