3

Can anyone think of a possible analytical solution of the following equation?

$x\left(1-0.2x^2\right)^{5/2}=constant$

I am not a mathematician, but, it seems to me that only numerical methods can help.

Thanks in advance.

TZakrevskiy
  • 22,980
user2536125
  • 221
  • There may be asymptotic solutions if the constant on the right-hand side is very large or very small. There may also be some bounds on where the roots may lie in the complex plane. Whether or not these are useful probably depends on your application. – Antonio Vargas Sep 17 '13 at 17:16
  • Hi @AntonioVargas and thanks for the answer. Your comment is extremely usefull, sice it can help to get a starting guess for the numerical algorithm. Can you please provide some references or links? PS: The constant is of the order $10^-1$ and $x$ in opinion, is of the order $10^-1$. – user2536125 Sep 18 '13 at 05:54
  • I think you can expect analytical solutions only in rare case, because the solutions to your problems are the roots of the polynomial $$x^{12} -25x^{11} +250 x^{12} - 1250 x^9 +3125 x^8 -3125 x^7 + 3125 c^2$$ which cannot expressed by radicals in general. – gammatester Sep 18 '13 at 09:23
  • That's what I was thinking....Now, what if I manage to guess one solution, is there a simple way to factorize, i.e; determine the remaining solutions? – user2536125 Sep 18 '13 at 12:42
  • You can use synthetic divison (http://en.wikipedia.org/wiki/Synthetic_division) or root deflation (search this on the web, see e.g. http://mathonweb.com/help_ebook/html/poly_2.htm) – gammatester Sep 18 '13 at 13:01
  • Possible solution what you suggested @gammatester , however , not very practical when we are talking about very large data. – user2536125 Sep 18 '13 at 13:55
  • Granted, but it can be done algorithmically with http://en.wikipedia.org/wiki/Polynomial_long_division (the remainder is zero for the root) – gammatester Sep 18 '13 at 14:04
  • $\large\left\vert x\right\vert \leq 5$. – Felix Marin Sep 25 '13 at 21:31
  • @FelixMarin I believe you mean $|x| \leq \sqrt{5}$. – Antonio Vargas Sep 25 '13 at 21:48
  • @AntonioVargas Yes: $\sqrt{5}$. See my answer below. – Felix Marin Sep 25 '13 at 23:31

2 Answers2

2

If you're looking to solve

$$ x\left(1-\tfrac{1}{5} x^2\right)^{5/2} = c $$

when $c$ and $x$ are very small then you can apply the Lagrange inversion formula (see, for example, my answer here) to find $x$ in terms of a power series in $c$. In the formula take

$$f(x) = \left(1-\tfrac{1}{5} x^2\right)^{-5/2}.$$

The first few terms of the series are

$$ x = c+\frac{1}{2}c^3+\frac{27}{40}c^5+\frac{481}{400}c^7+\frac{39151}{16000}c^9+\frac{4308003}{800000}c^{11}+\frac{7987003}{640000}c^{13}+\cdots $$

and truncating the series here gives a good underestimate of the root when $c < 1/2$ which gets better as $c \to 0$.

Here's a plot of the absolute error of this approximation with $c$ on the horizontal axis and a logarithmic scale on the vertical (error) axis.

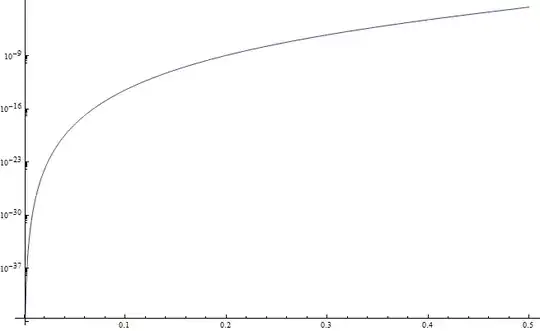
enter image description here

The approximation is still fairly good if we only use the first three terms of the series. Here's the error in that case:

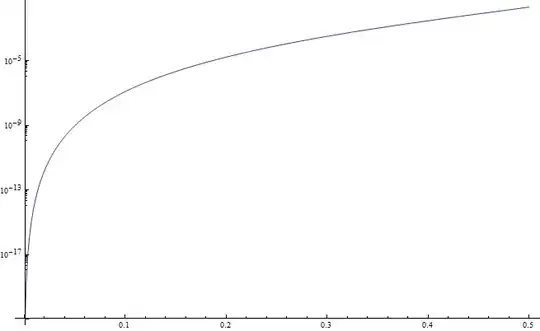
enter image description here

I'll comment a little bit more here about the (two) positive roots, both when $c \gtrapprox 0$ and when $c \lessapprox 125/216$.

The quantity $x\left(1-\tfrac{1}{5}x^2\right)^{5/2}$ is $0$ when $x=0$, increases to a max of $125/216$ when $x=\sqrt{5/6}$, then decreases to $0$ when $x=\sqrt{5}$. Due to the $5/2$ exponent this quantity is not real for $x>\sqrt{5}$. So (a) when $0<c<125/216$ the equation $x\left(1-\tfrac{1}{5}x^2\right)^{5/2}=c$ has exactly two real solutions, one $<\sqrt{5/6}$ and one $>\sqrt{5/6}$, (b) when $c=125/216$ there is exactly one real solution, namely $x=\sqrt{5/6}$, and (c) when $c>125/216$ there are no real solutions. See this plot:

enter image description here

We gave a series for the solution $< \sqrt{5/6}$ above. The solution $>\sqrt{5/6}$ can be approximated in a slightly different way when $c > 0$ is very small (and hence $x$ is very close to $\sqrt{5}$). We first note that $x\left(1-\tfrac{1}{5}x^2\right)^{5/2}$ is on the order of $(\sqrt{5}-x)^{5/2}$ when $x \approx \sqrt{5}$. If we then substitute $x = \sqrt{5}-y$ and assume a series solution of the form

$$ y = \sum_{k=1}^\infty a_k c^{\tfrac{2k}{5}}, $$

we can expand everything as a series and solve for the coefficients $a_k$ recursively to find that

$$ \begin{align} y&=\frac{5^{3/10}}{2}c^{2/5}+\frac{9}{8\cdot5^{9/10}}c^{4/5}+\frac{77}{400\cdot5^{1/10}}c^{6/5} \\ &\qquad +\frac{3289}{16000\cdot5^{3/10}}c^{8/5}+\frac{63}{256\sqrt{5}}c^2+\cdots \end{align} $$

and hence that the solution in question is approximately

$$ \begin{align} x&=\sqrt{5}-\frac{5^{3/10}}{2}c^{2/5}-\frac{9}{8\cdot5^{9/10}}c^{4/5}-\frac{77}{400\cdot5^{1/10}}c^{6/5} \\ &\qquad -\frac{3289}{16000\cdot5^{3/10}}c^{8/5}-\frac{63}{256\sqrt{5}}c^2+\cdots \end{align} $$

when $c \gtrapprox 0$. We can also perform a similar analysis in the regime where $c \lessapprox 125/216$ to find that our two real solutions are approximately

$$ \begin{align} x^{\pm} &= \sqrt{\frac{5}{6}} \pm \sqrt{\frac{6}{5}} \left(\frac{125}{216}-c\right)^{1/2}+\frac{1}{25} \sqrt{\frac{6}{5}} \left(\frac{125}{216}-c\right) \\ &\qquad \pm \frac{124}{625} \sqrt{\frac{6}{5}} \left(\frac{125}{216}-c\right)^{3/2}+\frac{5197}{78125}\sqrt{\frac{6}{5}}\left(\frac{125}{216}-c\right)^2 + \cdots. \end{align} $$

Community
  • 1
Antonio Vargas
  • 24,993
  • @AntonioVargas.....How come you have only odd powers in the expression, although the expression in your original post contains both even and odd powers of c? – user2536125 Sep 24 '13 at 17:05
  • @user2536125, it follows from the fact that a differentiable even function has slope $0$ at the origin. Since $f(x)$ is even so is $(f(x))^k$, and if $k$ is even then $\left(\frac{d}{dx}\right)^{k-2} (f(x))^k$ is even as well. Taking the derivative one more time and setting $x=0$ will then yield zero. In other words, if $k$ is even then $$\left[\left(\frac{d}{dx}\right)^{k-1} (f(x))^k\right]_{x=0} = 0,$$ so all of the terms involving even powers of $c$ drop out of the series given by the Lagrange inversion formula. – Antonio Vargas Sep 24 '13 at 17:14
  • Absolutely right, thanks alot for your help, because it did not only solve my problem, but also, get a better reult as did Matlab built in numerical algorithms. – user2536125 Sep 25 '13 at 08:49
  • But what if x and c are very small? will there be an alternative? – user2536125 Sep 25 '13 at 11:20
  • @user2536125 Glad to help. If $x$ and $c$ are very small then this approximation gets better and better. If you only used the first three terms of the approximation (i.e. $x \approx c + \tfrac{1}{2}c^3 + \tfrac{27}{40}c^5$) then my calculations in Mathematica say that this approximation is accurate to $13$ digits after the decimal point when $c=10^{-2}$ and $20$ digits when $c=10^{-3}$. In an ideal computing environment you could get more digits of accuracy if you used more terms of the approximation. – Antonio Vargas Sep 25 '13 at 13:10
  • for the time being, my problem is solved, however, curiosity makes me wonder if there are other approximations valid when c and x are larger. – user2536125 Sep 25 '13 at 14:54
  • I had wondered the same thing. I've edited my answer to include some of the results. – Antonio Vargas Sep 25 '13 at 21:25
0

$x\left(1 - 0.2x^{2}\right)^{5/2} = c\,\sqrt{5\,} = \mbox{constant}$. I ${\bf guess}$ $\left(1 - 0.2x^{2}\right) \geq 0$. Then, $\left\vert x\right\vert \leq \sqrt{5\,}\,$ and ${\rm sgn}\left(x\right) = {\rm sgn}\left(c\right)$. Define $\xi\ \ni\ 0 \leq \xi \leq 1$ and $x \equiv {\rm sgn}\left(c\right)\,\sqrt{5\xi\,}\,$:

$$ \sqrt{\xi\,}\,\left(1 - \xi\right)^{5/2} = \left\vert c\right\vert\,, \qquad \xi\left(1 - \xi\right)^{5} = c^{2} $$

The function ${\rm f}\left(\xi\right) \equiv \xi\left(1 - \xi\right)^{5}$ has its maximum value at $\xi_{M} = 1/6$. ${\rm f}\left(\xi_{M}\right) = 5^{5}/6^{6} \approx 0.0670$. When $\left\vert c\right\vert > 5^{5/2}/6^{3} \approx 0.2588$, there isn't any real solution for $\xi$. When $\left\vert c\right\vert < 5^{5/2}/6^{3} \approx 0.2588$ there are two solutions for $\xi$: 1) $< 1/6$ and 2) $> 1/6$. There are four solutions which can be found approximately:

$$ \begin{array}{ll} \left\vert c\right\vert \gtrsim 0\,, & \qquad & \xi \approx c^{2}\quad\mbox{and}\quad \xi \approx 1 - \left\vert c\right\vert^{2/5} \\[3mm] \left\vert c\right\vert \lesssim{5^{5/2} \over 6^{3}}\,, & \qquad & \xi \approx \xi_{M}\,\,\, \mp\,\,\, \sqrt{2\left[{\rm f}\left(\xi_{M}\right) - c^{2}\right] \over -{\rm f}''\left(\xi_{M}\right)} \end{array} $$ With this information, the numerical approach should be the $Bisection\ Method$.

Felix Marin
  • 89,464