Have this question, but have no answers in the book, so just wanted to check my progress.
Consider the following complex potential:
$$\Omega(z) = -\frac{k}{2\pi}\frac{1}{z}$$
Calculate the corresponding velocity potential, stream function and velocity field. Sketch the stream function.
Parameterising $z = re^{i\theta}$, I get: $\Omega(r,\theta) = -\frac{k}{2\pi r}(cos\theta - i\sin\theta)$; so I get the velocity potential and stream function as:
$\phi(r,\theta) = -\frac{kcos\theta}{2\pi r}$;
$\psi(r,\theta) = \frac{ksin\theta}{2\pi r}$
I'm not very sure about the velocity field. Is it just the two directions of the velocity potential?
Also not too sure about sketching the stream function. I converted back into Cartesian coords to get $\psi (x,y) = \frac{ky}{2\pi (x^2+y^2)}$ and started plugging in different y values and solving for different constants (setting $k=1$). Seems very long-winded? I got a rough sketch of:
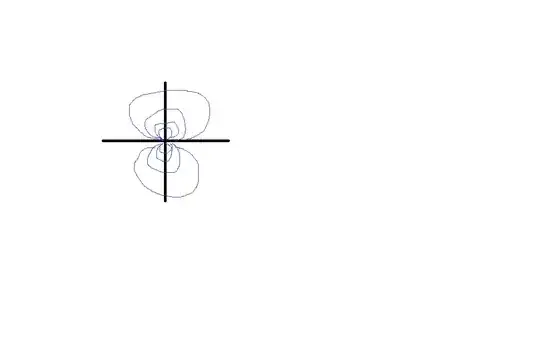
Any feedback appreciated! (And I'm no relation to Picasso in case anybody wondered)