Hi learning Lean I came cross the following property of category equivalence:
Definition An equivalence of categories cosnists of $(F, G, \eta, \epsilon)$ where $F: C \rightarrow D$ and $G: D\rightarrow C$ are functors and $\eta: 1_C \cong GF$, $\epsilon: FG\cong 1_D$ are natural isomorphisms.
and
Theorem if $F \Rightarrow FGF \Rightarrow F$ is identity, so is $G \Rightarrow GFG \Rightarrow G$.
The purpose of this theorem is for showing that the above definition can be equipped with the two triangle equalities in the above theorem, as said in the document of Lean's Mathlib4 Equivalence of categories.
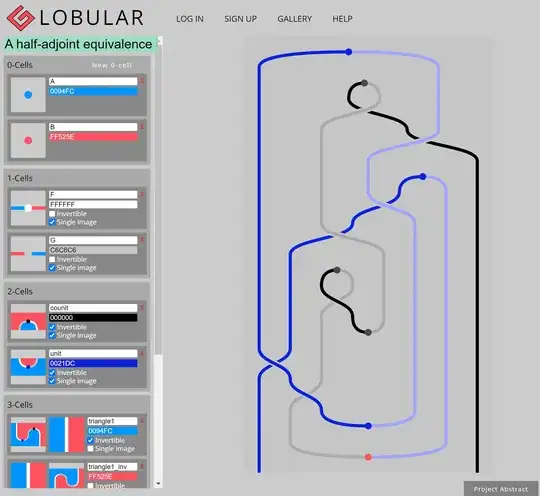
I proved it manually but I don't get the proof linked to http://globular.science/1905.001, which shown as a diagram bellow, found in the source code in here. What does the meaning of it? How to translate it to a plain English proof? Thank you for any helps, ideas and references for it!