Prove that no three of the six angles trisectors meet at one point

Question

I.e., that there are 12 distinct intersection points of the angle trisectors. $ABC$ is a triangle:

with its 6 angle trisectors. Prove that $M, N, O, P, Q, R, S, T, U, V, W, X$ (the trisector's intersections) are all distinct. The only formula I found about angle trisectors is Morley's Formula, saying that $PQU$ is equilateral.

Answer 1

Denote $\angle BAC = 3 \alpha$, $\angle CBA = 3\beta$ and $\angle ACB = 3\gamma$ and assume that $\alpha>\gamma$. If $BR$ passes through $M$ then by trig Ceva we have $$\frac{\sin 2\alpha}{\sin \alpha}\cdot \frac{\sin \beta}{\sin 2\beta} \cdot \frac{\sin 2\gamma}{\sin \gamma} = 1.$$ Using $\sin 2\xi = 2\sin \xi \cos \xi$ we get $$2\cos \alpha \cos \gamma = \cos \beta.$$ Since $\cos \frac \pi 3 = \frac 12$, we have $$2\cos \alpha \cos \gamma = 2\cos \beta \cos \frac \pi 3.$$ By $2\cos \xi \cos \zeta = \cos (\xi+\zeta) + \cos(\xi-\zeta)$ we obtain $$\cos(\alpha+\gamma) + \cos (\alpha - \gamma) = \cos(\beta+\frac\pi3) + \cos(\beta-\frac\pi3).$$ Since $\alpha+\beta+\gamma=\frac \pi 3$, $\cos (\alpha+\gamma)$ and $\cos(\beta-\frac \pi 3)$ cancel out which leads to $$\cos(\alpha-\gamma) = \cos(\beta+\frac\pi 3).$$ Since $\cos$ is injective on $[0,\pi]$, this means that $\alpha-\gamma = \beta+\frac \pi 3$, which is absurd: $\alpha-\gamma < \alpha < \frac \pi 3 < \beta+\frac \pi 3$.

You can prove in similar fashion that no other three lines concur.

Answer 2

Disclaimer : Not a direct answer but a methodology.

As your question can be understood as "how can I attack such an issue ?", I would like here to propose two combined tools for such questions involving angle bisectors in a triangle : trilinear coordinates $(u:v:w)$ (abbreviation here : t.c.) and their use with isogonal conjugation $(u:v:w) \leftrightarrow (\tfrac{1}{u}:\tfrac{1}{v}:\tfrac{1}{w})$.

I will show it through a configuration of 8 points (see figures 1 and 2) sharing some points with your own configuration.

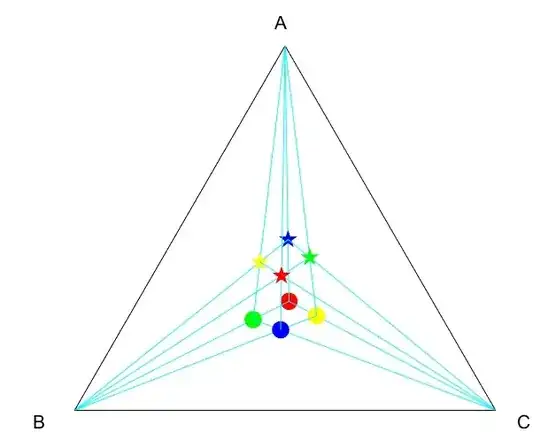
Fig. 1 : A case where the angles aren't trisected in 3 equal values (not a "Morley configuration").

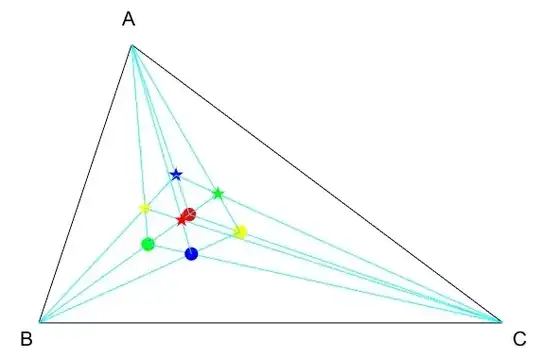
Fig. 2 : A Morley configuration for a general triangle.

This configuration is determined by a single point with t.c. $(u:v:w)$ in the following way (see the correspondence with Fig. 1 (and your own figure) :

$$\begin{cases} (u:v:w)&\text{red disk}\\ (\tfrac{1}{u}:v:w)&\text{blue star ; your point O}\\ (u:\tfrac{1}{v}:w)&\text{green disk ; your point S}\\ (u:v:\tfrac{1}{w})&\text{yellow disk}\\ (u:\tfrac{1}{v}:\tfrac{1}{w})&\text{blue disk ; your point U}\\ (\tfrac{1}{u}:v:\tfrac{1}{w})&\text{green star ; your point Q}\\ (\tfrac{1}{u}:\tfrac{1}{v}:w)&\text{yellow star ; your point P}\\ (\tfrac{1}{u}:\tfrac{1}{v}:\tfrac{1}{w})&\text{red star} \end{cases}$$

where two points with the same color are isogonal conjugates ; for example the yellow disk is conjugated with the yellow star (their t.c. are inverted componentwise).

Remarks :

1. This (2D!) points configuration can be considered as the perspective view of a cube represented with its 3 families of parallel edges prolongated until they meet resp. in $A,B,C$, playing the rôle of points at infinity.

2. The (extended) Morley configuration and its description in terms of t. c. can be found here.

Matlab program :

 function main;
    close all;
    set(gcf,'color','w');axis off;hold on;
    A=3*i+1;B=0;C=5;plot([A,B,C,A],'k');hold on;axis equal
    a=abs(B-C);b=abs(C-A);c=abs(A-B);
    cA=2*cos(aA/3);cB=2*cos(aB/3);cC=2*cos(aC/3);
    % u=0.7;v=0.8;w=0.9
    % For a Morley configuration :
    u=sqrt(cA/(cB*cC));
    v=sqrt(cB/(cC*cA));
    w=sqrt(cC/(cA*cB));
z=T2C(u,v,w,'or');plot([z,A,z,B,z,C],'c');
z=T2C(1/u,v,w,'pb');plot([B,z,C],'c');
z=T2C(u,1/v,w,'og');plot([C,z,A],'c');
z=T2C(u,v,1/w,'oy');plot([A,z,B],'c');
z=T2C(u,1/v,1/w,'ob');plot([z,A],'c')
z=T2C(1/u,v,1/w,'pg');plot([z,B],'c')
z=T2C(1/u,1/v,w,'py');plot([z,C],'c')
z=T2C(1/u,1/v,1/w,'pr');

% Sanity check : classical Morley triangle 
z=T2C(1,cA,cB,'*k');hold on
z=T2C(cC,1,cA,'*k');hold on
z=T2C(cB,cA,1,'*k')


function z=T2C(ta,tb,tc,g); % Trilinear to Cartesian coord.
    global A B C a b c;
    den=ata+btb+ctc;
    k1=ata/den;k2=btb/den;
    z=C+k1(A-C)+k2*(B-C);g2=g(2);
    plot(z,g,'MarkerSize',10,'MarkerFaceColor',g2);hold on;