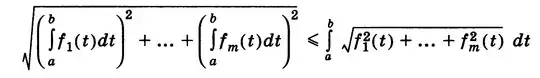Integral Jensen Inequality

Asked Mar 28 '24 at 21:33

Active Mar 28 '24 at 21:33

Viewed 40 times

I need to understand how does this equation derives from Jensen inequality ($\varphi(\frac{1}{b-a}\int_{a}^{b}f(x)dx) \leq \frac{1}{b-a}\int_{a}^{b}\varphi(f(x))dx$) It seems that I can show that $(\int_{a}^{b}f(t)dt)^2 \leq (b-a)\int_{a}^{b}(f(t))^2dt$ by applying the Jensens inequality if consider $\varphi(x)=x^2$ but I can't get the idea of proving the full inequality on the picture. Thanks in advance!

asked Mar 28 '24 at 21:33

bob

I will just mention that this is a special case of Minkowski's integral inequality. – Maximilian Janisch Mar 28 '24 at 21:53
This follows from a generalization of https://math.stackexchange.com/a/4880077/465145 to higher dimensions, which can be proved in the exact same way (or alternatively, using a higher dimensional version of Jensen’s inequality and the fact that norms are convex functions). – David Gao Mar 28 '24 at 23:09

Integral Jensen Inequality

0 Answers0