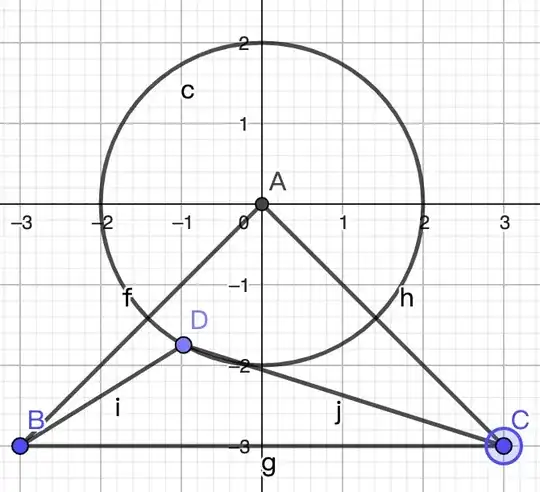
If $m^2+n^2=1$, find the maxmum of $\dfrac{5-4m}{5-4n}$.
The original question is to find the maximum of $\dfrac{BD}{CD}$. By simplifying the formula through cosine theorem, I get the above formula. The value should be equal to $\sqrt{\dfrac{5-4m}{5-4n}}$.
How to find the value? Any elegant geometric solutions are also welcomed.
Take $m = \sin \theta$ & $n=\cos \theta$.
Now put these values in the given expression and convert $\sin \theta$ & $\cos \theta$ into $\tan \left(\frac{\theta}2\right)$ using
$$\sin θ= \frac{2\tan(θ/2)}{1+\tan^2(θ/2)}$$
$$\cos θ = \frac{1-\tan^2(θ/2)}{1+\tan^2(θ/2)}$$ Now take $\tan(θ/2) = y$
The above expression becomes $f(y)$. For maxima, $\frac{\mathbb d}{\mathbb d y}f(y)=0$. Solve for $y$ and put this value of $y$ in $f(y)$.
(I'll write $x=m$ and $y=n$)
Lagrange multipliers gives the following group of equations
$$\begin{align} -\frac{4}{5-4y} + 2\lambda x = 0 \\ 4\frac{5-4x}{(5-4y)^2} + 2\lambda y = 0 \\ x^2 + y^2 = 1 \end{align} $$
Solving from first $\lambda = \frac{2}{x(5-4y)}$ and plugging it in second to get
$$ (5-4x)x = -y(5-4y) $$
This is an equation of a circle:
$$ \left(x-\frac{5}{8}\right)^2 + \left(y-\frac{5}{8}\right)^2 = \frac{25}{32} $$
So we're left with finding the intersections of this with the unit circle. They are
$$ x = \frac{2}{5} - \sqrt{\frac{17}{50}} \\ y = \frac{2}{5} + \sqrt{\frac{17}{50}} $$
(and vice versa gives the minimum).
It is surprising to see no answer using quadratic equations and their properties. Let us write $$r = \frac{4m-5}{4n-5}\iff 4n=\frac{4m-5}{r}+5$$
Substitute into $m^2+n^2=1$ to get a quadratic in $m$ which becomes: $$g(m):=16m^2(r^2+1)-40m(1-r)+25(1-2r)+9r^2=0$$ and since we need $m\in \mathbb R$ we put $\text{Disc}_m(g) \geq 0$. This means $$1600(r-1)^2-4\cdot 16(r^2+1)\cdot (9r^2-50r+25)\geq 0$$ This becomes upon expansion $$-64r^2(9r^2-50r+9)\geq 0\iff 9r^2-50r+9\le 0$$ Now note that $f(x):= 9x^2-50x+9$ has two real roots, viz $$x_0=\frac{25- 4\sqrt{34}}9$$ and $$x_1=\frac{25+4\sqrt{34}}9$$ Thus we need $(r-x_0)(r-x_1)\le 0$ which means $$r \in [x_0,x_1]$$ We conclude that $$\boxed{\max r = x_1=\frac{25+4\sqrt {34}}9}$$ $$\boxed{\min r = x_0 = \frac{25-4\sqrt{34}}9}$$
A geometric approach:
Draw a unit circle and a circle of radius $4$, and mark $D$ at $(5,5)$. Then for any point $(m,n)$ on the unit circle, $(4m,4n)$ lies on the outer circle, and $5-4m$ and $5-4n$ are the horizontal and vertical projections, illustrated for point $E$. The ratio you wish to maximize is the slope, which will be maximal at the point of tangency forming triangle $DGA$. We already have sides $AD,AG$ by construction, so the angle $DAG$ is $\arctan\frac{\sqrt{50}}{4}$ which is about $55.55$ degrees, and since the angle above the x-axis is $45$ degrees by construction, the angle under the x-axis is about $\alpha=10.55$ degrees. The coordinates of $m,n$ are $(\cos{\alpha},\sin{\alpha})$ which is about $(-0.9831,-0.1831)$, giving maximal slope of about $5.36$ (I'm fixing the negative signs mentally here, since I inadvertently made the construct in quadrant II). These values should be exactly those found by @ploosu2.
Let $m=\sin\theta$ and $n=\cos\theta.$ Since we are after the maximal value we may assume that $m\le 0$ and $n\ge 0.$ We want to maximize $$f(\theta)={4\sin\theta-5\over 4\cos\theta-5}$$ The numerator of the derivative $f'(\theta)$ is equal $$ 4\cos\theta(4\cos\theta-5)-(4\sin\theta-5)(-4\sin\theta)\\ =16\cos^2\theta -20\cos\theta-20\sin\theta+16\sin^2\theta\\ =4[4-5(\cos\theta+\sin\theta)] $$ Therefore $f'(\theta)=0$ if $\sin\theta+\cos\theta={4\over 5}.$ By taking into account $\sin^2+\cos^2\theta=1$ we get that both $\sin\theta_0$ and $\cos\theta_0$ are the solution of the quadratic equation $$5x^2-4x-{9\over 10}=0$$ Since we want $\sin\theta_0\le 0$ and $\cos\theta_0\ge 0$ then $$\cos\theta_0={4+\sqrt{34}\over 10},\quad \sin\theta_0={4-\sqrt{34}\over 10}$$
The maximum of the functions $f_{\pm}(x)=\frac{5\pm\sqrt{1-x^2}}{5-4x}$ on $[-1,1]$ is asked. The numerators of their first derivatives give the equations $5\sqrt{1-x^2}=\pm(5x-4)$ for critical points, respectively.
The solution of the equation belonging to $f_+$ gives the critical point $x=\frac{4+\sqrt{34}}{10}$ with the maximum value $\frac{25+4\sqrt{34}}{9}\approx 5.34>5$ on the interval $[-1,1]$. On the other hand, the maximum of $f_-$ is $5$ at one of the boundary points, namely $x=1$.
WolframAlpha gives more details.
WLOG $y=\dfrac{5-4\cos t}{5-4\sin t}$
$$\implies5-5y=4(\cos t-y\sin t)$$
Now $\sqrt{1+y^2}\le\cos t-y\sin t\le\sqrt{1+y^2}$
$\implies-\sqrt{1+y^2}\le\cos t-y\sin t\le\sqrt{1+y^2}$ $\implies-\sqrt{1+y^2}\le\dfrac{5-5y}4\le\sqrt{1+y^2}$
$\implies (5-5y)^2\le16(1+y^2)\iff9y^2-50y+9\le0$
Now the roots of $9y^2-50y+9=0$ are $\dfrac{50\pm\sqrt{50^2-4\cdot81}}{18}=\dfrac{25\pm4\sqrt{34}}9$
$\implies y\le\dfrac{25+4\sqrt{34}}9$
