Have a look at Fig. 1 modelizing the position of the extremity of a string rolled/unrolled along a convex polygon (here the particular case of a regular octagon) generating a kind of spiral (modelizing rather well a half-egg-shape) ?
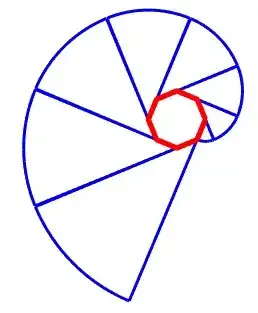
Fig. 1.
But one can obtain much general type of curves as one can see on Fig. 2 (see Matlab program below). Here, four different curves ("offsets" of the first one) are displayed just by changing the curve length.

Fig. 2.
Last but not least, being a Frenchman, I don't resist the pleasure to offer you a "croissant" (with eggs entering into its composition :)) :
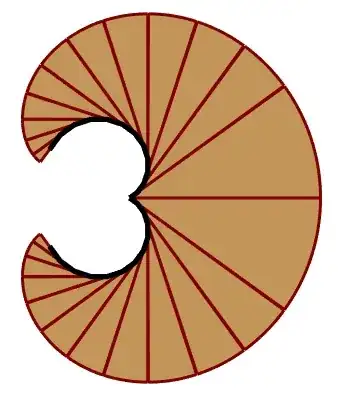
Fig. 3.
Matlab program (using complex numbers geometry) having generated figure 2 :
function main;
a=80;axis([-a,a,-a,a])
A=[0,pi/4,pi/3,pi/2,2*pi/3,pi,5*pi/4,3*pi/2,7*pi/4,2*pi];% sides polar angles
Lg=[1,1,3,2,7,1,4,5,20,20];% side lengths
V=Lg.*exp(A*i);A=[A,A(1)];Lg=[Lg,Lg(1)];L=sum(Lg);
LA=length(A);
Pt=cumsum(V);% points, obtained by cumulating vectors
for k=0:2:6
C=[]; % curve
M=L+k;
for k=1:LA-2
T=cs(Pt(k),M,A(k),A(k+1));
C=[C,NaN,T];
M=M-Lg(k+1);
end;
plot(C,'b','linewidth',2);hold on;
end;
plot(Pt,'color','r','linewidth',4);hold on
%%%
function T=cs(ce,r,t1,t2);% circular sector
s=sign(t2-t1);
T=ce+r*[0,exp(i*(t1:s*0.005:t2)),0];
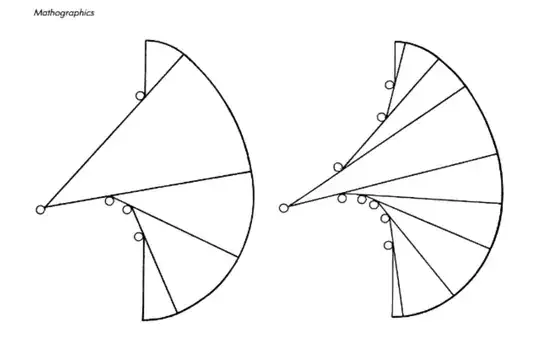



What I'm looking for are the parametric equations of the 'string, pins, and pen' involute given by Dixon (see image attached in post).
– Johnny Mar 25 '24 at 23:36