For fixed real numbers $a,b,c,d$ define the map $f : \mathbb{R}^2 \to \mathbb{R}^2$ by $$f : (x, y) \longmapsto (\phi(ax) + b \cdot \phi(ay),\hspace{1em} \phi(cx) + d \cdot \phi(cy)), \qquad \phi(z) := \sin(z).$$
Given a point $(x_0, y_0) \in \mathbb{R^2}$ we consider its orbits under the iterates of $f$, i.e., $$\Omega := \{f^n(x_0, y_0) \;\vert\; n \in \mathbb Z_{>0} \}$$
Here is a question I asked myself after plotting some of these sets $\Omega$:
Is it true that for $x_0 = y_0 = 1$ and $(a, b, c, d) = (3, -1, 3, -3)$, the closure $\overline{\Omega} \subset \mathbb{R}^2$ is equal to the parallelogram $P$ with vertices $\pm (0, 2), \pm (2, 4)$ ?
Thoughts:
This is confirmed experimentally (using SAGE, see the code below), using $n \leq 500000$ points:
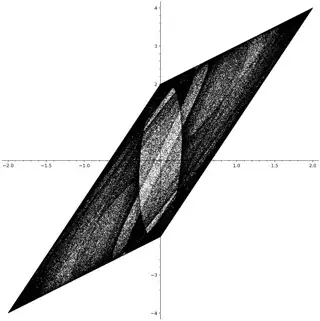
Since the sine function takes values in $[-1, 1]$, it is clear that $\Omega$ is contained in the parallelogram $P$ (hence $\overline{\Omega} \subset P$) : indeed we have $$f(x, y) = (\sin(3x) - \sin(3y), \sin(3x) - 3 \sin(3y)) = \begin{pmatrix} 1 & -1 \\ 1 & -3 \end{pmatrix} \begin{pmatrix} \sin(3x) \\ \sin(3y) \end{pmatrix}$$ and the image of the square $[-1, 1]^2$ under the linear map $\begin{pmatrix} 1 & -1 \\ 1 & -3 \end{pmatrix}$ is $P$.
The appearance of a parallelogram is probably explained by the fact that $a = c$. In general, we obtained "fractal" objects like in this question asked some years ago by the same author: Properties of King's Dream fractal
When we replace $\sin(x)$ by $\phi(x) = \{ 1.5 x \}$ (where $\{ … \}$ denotes the fractional part), we also get a parallelogram for $(a, b, c, d) = (3, -1, 3, -3)$ but NOT for $(a, b, c, d) = (1, -1, 1, -2)$.