Why does T = S1 work for conics?

Question

If we have a conic with equation: $ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0$ or S =0, and a point $P(x_1, y_1)$.

Then the equation of the chord with P as its midpoint is given by T = $S_1$.

$S_1$ is obtained by plugging point P in S. ($S_1$ = $ax_1^2 + 2hx_1y_1 + by_1^2 + 2gx_1 + 2fy_1 + c = 0$)

The 'T' form of an equation can be obtained by replacing:
$$x^2 \rightarrow xx_1$$ $$y^2 \rightarrow yy_1$$ $$x \rightarrow \frac{x + x_1}{2}$$ $$y \rightarrow \frac{y + y_1}{2}$$ $$xy \rightarrow \frac{xy_1 + x_1y}{2}$$

I don't understand how this works! Could someone help me understand why it does?

Edit: The slope of the chord somehow equals the derivative of the conic at point $(x_1, y_1)$. Can someone explain how that happens?

Answer 1

Here is a graphical representation in the case of an ellipse :

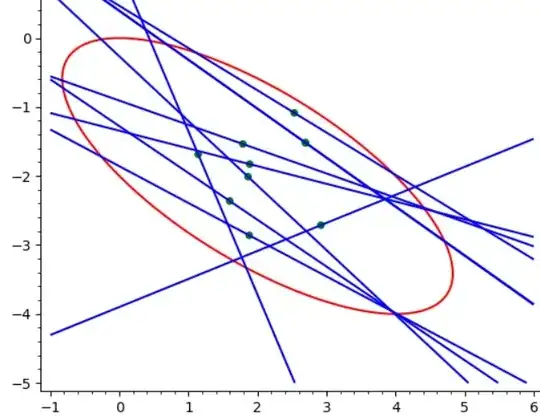
*Fig. 1.$

1. First version : analytic geometry calculations.

Being given the equation of the conic

$$ax^2 + 2hxy + by^2 + 2gx + 2fy + c\tag{*}$$

Let $U=\pmatrix{u\\v}$ be a directing vector of the chord, allowing its parameterization under the form :

$$\begin{cases}x&=&x_1+pu\\y&=&y_1+pv\end{cases}\tag{**}$$

The coordinates $(x,y)$ of the intersection points $P_1$ and $P_2$ of the chord with the conic curve will verify the expression obtained by "plugging" the expressions of $x$ and $y$ given by (**) into (*) giving rise to a quadratic polynomial in variable $p$:

$$Ap^2+2Bp+C=0 \ \text{with} $$ $$\begin{cases}A&=&au^2 + 2huv + bv^2\\B&=& u(ax_1+hy_1+g)+v(hx_1+by_1+f)\\C&=&ax_1^2 + 2hx_1y_1 + by_1^2 + 2gx_1 + 2fy_1 + c\end{cases}\tag{1}$$

Observe now that point $P_1$ is the midpoint of the chord iff the intersection points $Q$ and $Q"$ correspond to two opposite values of $p,-p$. It amounts to say that the sum of the roots of quadratic equation (1) is equal to zero, otherwise said that the central coefficient $2B$ is zero.

Relationship $B=0$ considered as a dot product equal to $0$ expresses the geometrical fact that :

$$U=\pmatrix{u\\v} \ \text{is orthog. to} \ N:=\pmatrix{ ax_1+hy_1+g\\hx_1+by_1+f}\tag{2}$$

$N$ being a normal vector to the chord, the equation of this chord is :

$$(x-x_1)(ax_1+hy_1+g)+(y-y_1)(hx_1+by_1+f)=0\tag{3}$$

Besides, equation $T=S_1$, when expanded, is :

$$axx_1 + h(xy_1+x_1y) + byy_1 + g(x+x_1) + f(y+y_1) + c=ax_1^2 + 2hx_1y_1 + by_1^2 + 2gx_1 + 2fy_1 + c\tag{4}$$

which can be put under the form :

$$x(ax_1+hy_1+g)+y(hx_1+by_1+f)=x_1(ax_1+hy_1+g)+y_1(hx_1+by_1+f)\tag{5}$$

Now compare (3) and (5).

---

Second version, with a vectorial formulation having the advantage of more compact notations.

Expression (*) can be given the form of a quadratic equation under the form :

$$X^TQX+2V^TX+c=0 \ \text{with} \ Q=\pmatrix{a&h\\h&f}, \ \ V=\pmatrix{g\\f}, \ X=\pmatrix{x\\y}\tag{6}$$

Expression (**) becomes $X=X_1+pU$ ; plugging it into (6) gives :

$$(X_1+pU)^TQ(X_1+pU)+2V^T(X_1+pU)+c=0$$

$$X_1^TQX_1+2pU^TQX_1+p^2U^TQU+2V^TX_1+2pV^TU+c=0$$

$$p^2 \underbrace{U^TQU}_A + 2p\underbrace{U^T(QX_1+V)}_B+\underbrace{(X_1^TQX_1+c)}_C=0$$

It is exactly numerical quadratic equation (1) (check it !). In particular, setting the coefficient $2B$ of $p$ to $0$, as before, we retrieve the fact that vector $U$ is orthogonal to :

$$QX_1+V=\pmatrix{a&h\\h&f}\pmatrix{x_1\\y_1}+\pmatrix{g\\f}=\pmatrix{ax_1+hy_1+g\\hx_1+by_1+f}\tag{7}$$

as obtained in (2).

Besides, let us express $S_1$ and $T$ under their resp. vectorial expressions :

$$\begin{cases}S_1 &:& X_1^TQX_1+2 X_1^TV+c\\T &:& X^TQX_1+ (X+X_1)^TV+c\end{cases}$$

Equating them, and simplifying, we get :

$$(X-X_1)^TQX_1+(X-X_1)^TV=0$$

$$(X-X_1)^T(QX_1+V)=0$$

which is the equation of a line passing through $X=X_1$ with normal vector $QX_1+V$ as "imposed" by (7) ! QED.

---

Edit : I answer your question about the fact that the normal vector to the chord is "rather surprisingly"

$$QX_1+V$$

i.e., equal (up to a $2$ factor) to the gradient of expression (6) computed in point $X_1$.

Have a look at figure 2 featuring a conic curve, and a point $X_1$ which is the midpoint of a chord found by the $T=S_1$ method

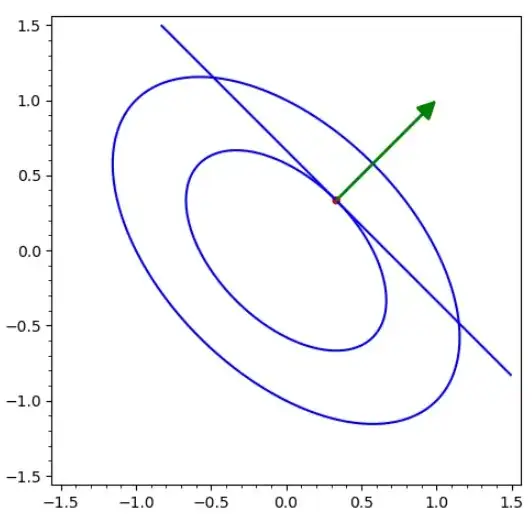
Fig. 2. Homothetic curves $Q(x,y)=1$ and $Q(x,y)=1/3$ with $Q(x,y)=x^2+xy+y^2$ and $(x_1,y_1)=(1/3,1/3)$.

This chord is in fact tangent to a homothetical ellipse to the initial ellipse : no surprize that the gradient at point $X_1$ is orthogonal to the tangent to the curve.

Answer 2

The given equation of the conic is

$a x^2 + 2 h x y + b y^2 + 2 g x + 2 f y + c = 0 $

If we define $p = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $

Then the above conic equation can be written in linear algebra style matrix-vector form as follows

$ p^T Q p = 0 $

where $ Q = \begin{bmatrix} a && h && g \\ h && b && f \\ g && f && c \end{bmatrix} $

Suppose, you have two points $p_1$ and $p_2$ on this conic, and define their midpoint as $ p' = \dfrac{1}{2} (p_1 + p_2) $, so that $p_2 = 2 p' - p_1 $

Since $p_2$ is on the conic, then

$ p_2^T Q p_2 = 0 $

But $p_2 = 2 p' - p_1$ , so

$ (2 p' - p_1)^T Q (2 p' - p_1) = 0 $

Multiply this out, you get

$ 4 p'^T Q p' - 4 p'^T Q p_1 + p_1^T Q p_1 = 0 $

Since $p_1$ is on the conic as well, then $p_1^T Q p_1 = 0 $, therefore the above equation reduces to

$ p'^T Q p' = p'^T Q p_1 $

Similarly, we can show that

$ p'^T Q p' = p'^T Q p_2 $

Now take an arbitrary point $q$ on the chord connecting $p_1$ and $p_2$, then

$ q = (1 - \lambda) p_1 + \lambda p_2 $

Pre-multiply $q$ by $p'^T Q$, you get

$ p'^T Q q = p'^T Q ( (1 - \lambda) p_1 + \lambda p_2) \\ = (1 - \lambda) p'^T Q p_1 + \lambda p'^T Q p_2 \\ = p'^T Q p' $

We have shown that the equation of the chord is

$ p'^T Q p' = p'^T Q q $

Since $p' = (x_1, y_1)$ , then $p'^T Q p' = S_1$

And $T = p'^T Q q = a x_1 x + h (x_1 y + x y_1) + b y_1 y + g (x + x_1) + f(y+y_1) + c $

$T$ can be re-arranged as follows

$T = p'^T Q q = a x_1 x + 2 h \left( \dfrac{ x_1 y + x y_1 }{2} \right) + b y_1 y + 2 g \left( \dfrac{x + x_1}{2} \right) + 2 f \left( \dfrac{y + y_1}{2} \right) + c $

which is the desired substitution.