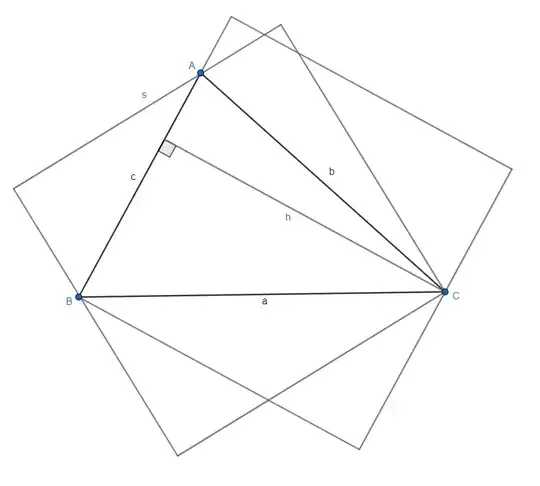
In the attached figure, your second triangle is red color and your first one is the same black color. You have $$\begin{cases}a\cos(t)=s\\a\cos(u)=h\end{cases}\Rightarrow \frac{s}{h}=\frac{\cos(t)}{\cos(u)}$$ Since $\triangle{ABC}$ is acute we have three possibilities
$$ s\lt h\iff \cos(t)\lt\cos(u)\iff t\gt u\\s\gt h\iff \cos(t)\gt\cos(u)\iff t\lt u\\s=h\iff t=u$$ Obviously these possibilities mean respectively black is bigger,red is bigger and both are equal.
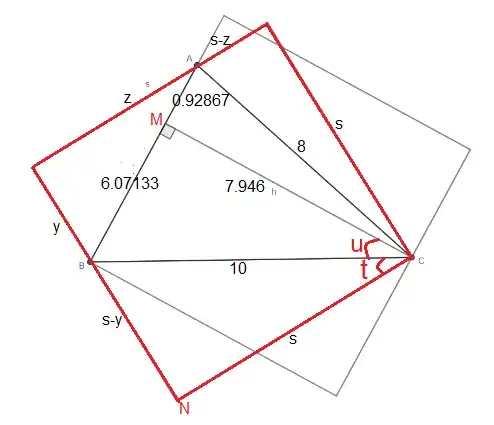
In the figure there are particular values to verify the size of concerned squares with $(a,b,c)=(10,8,7)$ and the literal calculation is similar but more difficult to manipulate.
We have $h\approx7.946$; the value of $s$ is not hard to determine; we have the system of three unknowns in which we eliminate $y$ and $z$ $$ y^2+z^2=7^2\\s^2+(s-z)^2=8^2\\s^2+(s-y)^2=10^2$$ We get $s\approx7.91643$ and $s\approx 3.4658$ so the black square is bigger.
Note the values of $h$ and $s$ are near. There are positions for $s\lt h$ and $s\gt h$ for which it is impossible the construction of squares such as asked but I not explain about it.