0

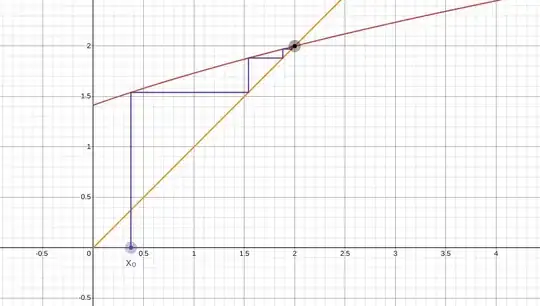
Define the sequence $(x_n)_{n \geq 0}$ with $x_0 >0$ and recursive equation $x_{n+1} = \sqrt{2+x_n}$ for all $n \geq 0$. I wish to determine the limit of the sequence $(x_n)_{n \geq 0}$ in terms of the parameter $x_0 \in (0, \infty)$.

If $x_0 < 2$, then $x_n > 0, (\forall)n \geq 0$, $x_n < 2, (\forall)n \geq 0$ and $(x_n)_n$ is strictly increasing. By Weierstrass' property, there exists $\ell = \lim_{n \to \infty} x_n \in \mathbb{R}$. Taking the limit, obtain $\ell^2-\ell-2=0$ with solutions $\ell \in \{-1,2 \}$. But since the $x_n>0, (\forall)n \geq 0$, $\ell \geq 0$ so $\lim_n x_n=2$.

If $x_0=2$, then $x_n=2, (\forall)n \geq 0$ constant sequence, so $\lim_n x_n=2$.

If $x_0>2$, then $x_n > 0, (\forall)n \geq 0$ and $(x_n)_n$ is strictly increasing. However, because $x_0>2$ we would have $x_n > 2, (\forall)n \geq 0$. But we know already that the only possible limit points of the sequence are $\lim_n x_n \in \{ -1,2, \pm \infty \} \subset \overline{\mathbb{R}}$, so does that mean the sequence diverges or am I missing something?

In conclusion, the question is: How do I analyse the sequence when $x_0>2$? Is the sequence divergent?

Darius Chitu
  • 447
  • See https://math.stackexchange.com/questions/115501/limit-of-the-nested-radical-x-n1-sqrtcx-n and the questions linked to it. – Martin R Mar 14 '24 at 17:53

2 Answers2

1

You've made a mistake somewhere. For $x_{n+1} = \sqrt{2 + x_n}$, and assuming that all $x_n > 0$,

  • $x_{n+1} > x_n$ for $x_n < 2$, and
  • $x_{n+1} < x_n$ for $x_n > 2$.

So in either case $x_{n+1}$ is closer to $2$ than $x_n$ (either increasing from below or decreasing from above).

Why? Let's look at the $x_n > 2$ case. \begin{align} x_n > 2 &\implies x_n - 2 > 0 \quad\text{and}\quad x_n + 1 > 0 \\ &\implies 0 < (x_n - 2)(x_n + 2) < x_n^2 - x_n - 2 \\ &\implies 2 + x_n < x_n^2 \\ &\implies \sqrt{2 + x_n} < x_n \\ &\implies x_{n+1} < x_n \end{align}

The $x_n < 2$ case is similar, noting that for $0 < x_n < 2$, we're between the two roots of the quadratic, so it's value is negative.

There's a more systematic way to think about this for recursively defined sequences near a fixed point. Suppose that $x_{n+1} = f(x_n)$ for some function $f$ with fixed point $x = L$: i.e., $f(L) = L$. We get convergence if

  • $x_{n+1} > x_n$ for $x_n < L$, and
  • $x_{n+1} < x_n$ for $x_n > L$,

or in other words if

  • $f(x) > x$ for $x < L$, and
  • $f(x) < x$ for $x > L$

on some interval around $L$. In your example, this interval is $(0, \infty)$.

You can see in a cobweb plot that as long as the graph $y = f(x)$ is increasing around $x = L$ but more slowly than $y = x$ (or decreasing but more slowly than $1$ in magnitude), then each iterate is closer to $L$ than its predecessor. Each vertical step connects $(x_n, x_n)$ to $(x_n, x_{n+1})$, and each horizontal step connects $(x_n, x_{n+1})$ to $(x_{n+1}, x_{n+1})$ so that the $x$-coordinate is ready to evaluate again in the function $f$.

Here's an illustration that is interactive. You can drag the initial value $x_0$ on the $x$-axis or modify the function $f$.

Cobweb plot of iterates.

If $f$ happens to be differentiable, it turns out that as a consequence of the Mean Value Theorem:

If $|f'(L)| < 1$, then the sequence of iterates converges to $L$ on this interval.

In our case, $$ f'(x) = \dfrac{1}{2\sqrt{2 + x}} < 1, $$ which is equivalent to $x > -\frac74$, which is certainly satisfied for all positive $x$.

Sammy Black
  • 25,273
1

The sequence converges for all $x_0\in \mathbb{R}^+$ to $2$. Here is an approach with closed-form solution.

For $x_0>2$: Denote $x_n = 2\cdot \cosh(\theta_n)$ then $$\begin{align} &\iff2\cdot \cosh(\theta_{n+1}) = \sqrt{2+2\cdot \cosh(\theta_n)} =\sqrt{4\cosh^2\left(\frac{\theta_n}{2} \right)} = 2\cosh\left(\frac{\theta_n}{2} \right)\\ &\iff \cosh(\theta_{n+1}) = \cosh\left(\frac{\theta_n}{2} \right)\\ &\iff \theta_{n+1} = \frac{\theta_n}{2} \\ &\implies \theta_n = \frac{\theta_{n-1}}{2}=...=\frac{\theta_0}{2^n} \end{align}$$ We deduce then $$\color{red}{x_n = 2\cdot \cosh\left(\frac{\text{arccosh}(x_0)}{2^n} \right)}$$ Because $\frac{\text{arccosh}(x_0)}{2^n}\xrightarrow{n\to+\infty}0$, we have then $x_n\xrightarrow{n\to+\infty}2$

For $x_0<2$: Denote $x_n = 2\cdot \cos(\theta_n)$, by the same method we have the closed form solution of $x_n$ $$\color{red}{x_n = 2\cdot \cos\left(\frac{\text{arccos}(x_0)}{2^n} \right)}$$ And the sequence converges also to $2$.

NN2
  • 15,892