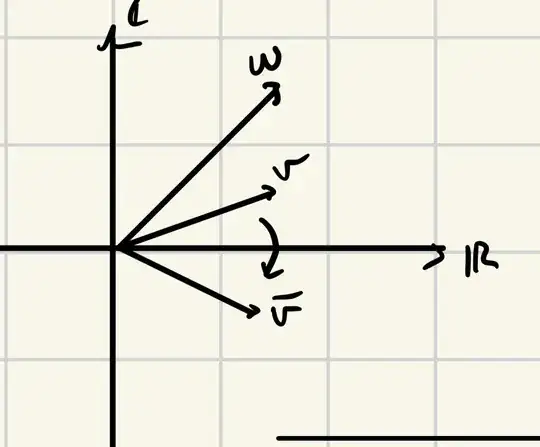
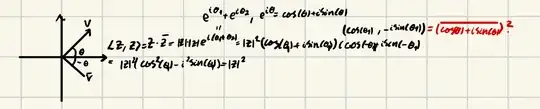We define the standard inner product on the vector space $\mathbb{C}$ over the field $\mathbb{C}$ as the function $\langle \cdot, \cdot \rangle: \mathbb{C} \times \mathbb{C} \to \mathbb{C}$ via $\langle \cdot, \cdot \rangle:(\boldsymbol{u}, \boldsymbol{v}) \mapsto \boldsymbol{u} \boldsymbol{\bar{v}}$. This notation can be cumbersome so we denote $\langle \cdot, \cdot \rangle((\boldsymbol{u},\boldsymbol{v}))$ as $\langle \boldsymbol{u},\boldsymbol{v} \rangle$. We can check that this satisfies the defining properties of an inner product (namely conjugate symmetry, linearity in the first argument, and positive-definiteness). The inner product $\langle \boldsymbol{w}, \boldsymbol{v}\rangle$ is computed as $\boldsymbol{w} \boldsymbol{\bar{v}}$ and not $\boldsymbol{w} \boldsymbol{v}$. It follows that the inner product between $\boldsymbol{w}$ and $\boldsymbol{\bar{v}}$ is $\langle \boldsymbol{w}, \boldsymbol{\bar{v}}\rangle = \boldsymbol{w} \boldsymbol{\bar{\bar{v}}}=\boldsymbol{w} \boldsymbol{v}$, which is not generally equal to the inner product between $\boldsymbol{w}$ and $\boldsymbol{v}$, $\langle \boldsymbol{w}, \boldsymbol{v}\rangle = \boldsymbol{w} \boldsymbol{\bar{v}}$.
I think a potential source of confusion is coming from introducing the "dot product" function $\cdot: \mathbb{C} \times \mathbb{C} \to \mathbb{C}$ via $\cdot:(\boldsymbol{u},\boldsymbol{v}) \mapsto \boldsymbol{u} \boldsymbol{v}$. It is important to note that $\cdot$ is not another inner product on the vector space $\mathbb{C}$ over $\mathbb{C}$ because it does not have the conjugate symmetry and positive-definiteness properties. However, one can write $\langle \boldsymbol{w}, \boldsymbol{v}\rangle=\boldsymbol{w} \cdot \boldsymbol{\bar{v}}$, meaning that the inner product of $\boldsymbol{w}$ and $\boldsymbol{v}$ is the dot product of $\boldsymbol{w}$ and $\boldsymbol{\bar{v}}$. It is incorrect though to say that the inner (dot) product of $\boldsymbol{w}$ and $\boldsymbol{v}$ is the inner (dot) product of $\boldsymbol{w}$ and $\boldsymbol{\bar{v}}$.
Therefore, the inner product of $\boldsymbol{v}$ and $\boldsymbol{\bar{v}}$ is not $\lvert \boldsymbol{v}\rvert^2$. It is $\boldsymbol{v}\boldsymbol{v}=\boldsymbol{v}^2$. The dot product of $\boldsymbol{v}$ and $\boldsymbol{\bar{v}}$ is $\lvert \boldsymbol{v}\rvert^2$. Distinguishing between the standard inner product and dot product is important here.