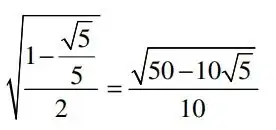I've been stuck on simplifying this nested radical. I've included a snapshot of the problem and solution that is in the trigonometry book that I am studying.
I've omitted the actual trig problem and just posted a pic of the part that is stumping me. I get the first part correctly but the second part of the equation (the actual correct answer according to the book) is what is stumping me.
I don't know if the book is wrong but any help would be appreciated.
You can work from the inside outward. Start by simplifying the fractions in the radical: $$ \sqrt{\dfrac{1-\dfrac{\sqrt5 }5}2}=\sqrt{\dfrac{\dfrac 5 5 -\dfrac{\sqrt5 }5}2}=\sqrt{\dfrac {5 -\sqrt5 }{10}} $$ Then, you can remove the radical from the denominator: $$ \sqrt{\dfrac {5 -\sqrt5 }{10}}=\dfrac{ \sqrt{5 -\sqrt 5 }}{\sqrt{10}}=\dfrac {\sqrt{10}}{\sqrt{10}}\dfrac{ \sqrt{5 -\sqrt 5 }}{\sqrt{10}}=\dfrac{\sqrt{10} \sqrt{5 -\sqrt 5 }}{10} $$ Finally, combine the radicals in the numerator: $$ \dfrac{ \sqrt{50 -10\sqrt 5 }}{10} $$
I find it easier to go backwards: $\dfrac{\sqrt{50-10\sqrt5}}{10}=\sqrt{\dfrac{50-10\sqrt5}{100}}=\sqrt{\dfrac{1-\dfrac{\sqrt5 }5}2}.$
This equality does not involve denesting radicals, but for those see this question.
$$\sqrt{\frac{1-\frac{\sqrt{5}}{5}}{2}} = \sqrt{\frac{(1-\frac{\sqrt{5}}{5})\cdot 50}{2 \cdot 50}} = \sqrt{\frac{50-10\sqrt{5}}{100}} = \frac{\sqrt{50-10\sqrt{5}}}{10}$$
$\sqrt {\frac{\frac{\sqrt 5}{\sqrt 5} - \frac{1}{\sqrt 5}}{2}} = \sqrt{\frac{\sqrt 5 - 1}{2 \sqrt 5}} = \sqrt{\frac{\Phi}{\sqrt 5} - \frac{1}{{\sqrt5}}} = \sqrt {\frac{\Phi - 1}{\sqrt 5}}$
Can you please post the problem.
