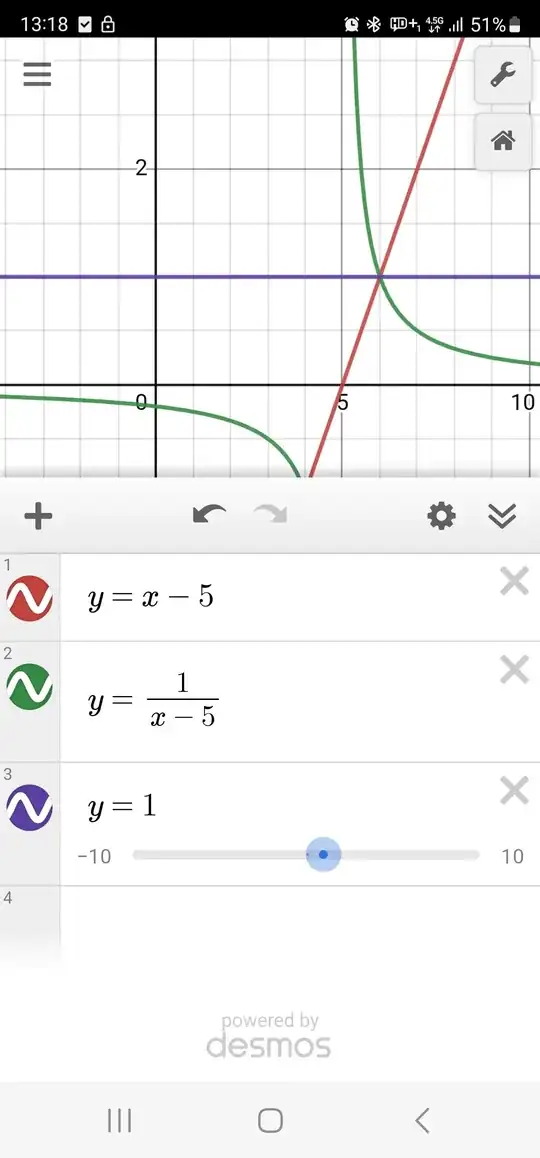
There's something I can't quite wrap my head around, and I am not satisfied with my professor's "that's just defined that way" answer. So suppose we have:
$$f_1(x) = x - 5$$
$$f_2(x) = \frac{1}{x - 5}$$
$$f_3(x) = 1$$
By simple algebra, we can see that $f4(x) = f_1(x) \cdot f_2(x) = f_3(x)$
What I mean is the rational function we get from dividing $x - 5$ by $x - 5$ is the same as the constant function $y = 1$
Now I like to look at functions graphically to understand them. So we can clearly see that $f_1(5) = 1$ and $f_2(5)$ is not defined. So how come, when we multiply these two functions, we end up with a function (or a curve) that is defined at point $x = 5$. By logic, on $x = 5$, we should have $0/0$, which is undefined. But here it just takes the value $1$. How come?
Visuals to better understand whats bugging me:
I would appreciate if your answer addresses this logically (or rather conceptually), not as a plain mathematical proof using algebra. I too, know, that algebraically speaking $(x - 5)/(x - 5)$ is just $1$, but thinking of functions visually rather than algebraically, this does not look convincing at all.