Is it true that [if the premises are false, the conclusion is true]?

Question

My question is, is my proof correct in concluding "If the premises are false, then the conclusion is true"?

Please see if my proof is correct

Is my proof of [If the premises are false, the conclusion is true] correct?

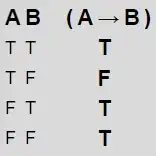
If the premises are false, the conclusion is false.

Statement 1 is false

because

I am cup. cup is an animal. i am an animal

The premise (I am cup, cup is an animal) is false, but the conclusion (I am an animal) is true.

If there is even one counterexample, the proposition is false.

Therefore, proposition 1 is false

Negation of proposition 1 is true.

The negation of (p->q) is (p and not q)

The negation of proposition 1 is

The premise is false and the conclusion is true.

Proposition 2 is true

If (p and q) are true then (p->q) is true

thus

If the premises are false, the conclusion is true.

Statement 3 is true

for example

I am a cup. cup is god. I am a God

Since the premise (I am a cup) is false, the conclusion (I am God) is true.

If the premises are false then the assertion that the premises imply the conclusion is true. However, you cannot deduce that the conclusion is true. — José Carlos Santos, Mar 07 '24 at 11:49
Your final argument is formally correct, but if the premises are false, as you can see, the conclusion can be false. — Mauro ALLEGRANZA, Mar 07 '24 at 12:00
@MauroALLEGRANZA if so, then how final argument can be correct? — Display name, Mar 07 '24 at 12:10
You have to understand the difference between a [formally correct argument](https://iep.utm.edu/val-snd/9 and a true conclusion. A conclusion is true if we prove it with a formally correct argument using true premises. In your case, the premises are false. — Mauro ALLEGRANZA, Mar 07 '24 at 13:12
Example of valid arguement: Santa Claus does not exist. God is Santa Claus. Therefore God does not exist. Now we have two correct arguments proving that God does not exist and that God exists (because you exist). — Mauro ALLEGRANZA, Mar 07 '24 at 13:13
See on philosophy: https://philosophy.stackexchange.com/questions/34082/why-are-conditionals-with-false-antecedents-considered-true — aschepler, Mar 07 '24 at 13:40
And note the difference between "the conclusion is true" and "the implication is true". — aschepler, Mar 07 '24 at 13:43
@Displayname I'm struggling to comprehend how you inferred Proposition 3 from the preceding lines, all of which are correct. In any case, as explained in Understanding implication, a false premise in an argument does not necessarily imply that the conclusion is true: when the premise P is false, it is the conditional P→C—not the conclusion C—that must be true! This common confusion arises from informally referring to both P→C and C as the "implication" in the argument. — ryang, Mar 07 '24 at 14:18

Bram28 · Answer 1 · 2024-03-07T13:51:13.890

Proposition 1. If the premises of an argument are false, then the conclusion is false.

No. Your counterexample works. Here is an another one:

"Snow is yellow. Therefore, bananas are yellow"

False premises, true conclusion, so proposition 1. is false.

Proposition 2. If the premises of an argument are false, then the conclusion is true.

No. Here is a counterexample

"Snow is yellow. Therefore, bananas are purple"

False premises, false conclusion, so proposition 2. is false as well.

But wait! I can hear you say. These aren't valid arguments! Well, you didn't say anything about that. But fine, let's consider two more propositions:

Proposition 3. If the premises of a valid argument are false, then the conclusion is false.

Again, your counterexample works. Here is an another one:

"Snow is yellow. Snow and bananas have the same color. Therefore, bananas are yellow"

False premises, true conclusion, so proposition 3. is false.

Proposition 4. If the premises of a valid argument are false, then the conclusion is true.

No. Here is a counterexample

"Snow is purple. Snow and bananas have the same color. Therefore, bananas are purple"

False premises, false conclusion, so proposition 4. is false as well.

The only combination that can't be is to have a valid argument with true premises and a false conclusion. Everything else is perfectly possible.

Dan Christensen · Answer 2 · 2024-03-08T03:20:35.963

If the premises are false, the conclusion is true.

Not exactly. For any propositions $A$ and $B$, if $A$ is false, then the implication $(A \to B)$ is true:

$~~~~~~(\neg A \to (A \to B))$

We cannot infer from this result that $B$ is true, or that it is false.

The Truth Table

$A$ is false on row 3 and 4 of this table. There, the implication is true (column 3), regardless of the truth value of $B$.

Formal Proof Using a Form of Natural Deduction

Here, we prove: ~A => [A => B]

Note that on line 6, we do indeed infer that $B$ is true. This, however, is an intermediate result. At that point in the proof, the premises on lines 1 and 2 have yet to be discharged. The proof is not complete as long as one or more premises are not discharged. On line 7, we discharge the premise on line 2 to obtain the conclusion: A => B. On line 8, the premise on line 1 is discharged to obtain the final conclusion: ~A => [A => B].

Plain text version of proof:

1   ~A
    Premise
2   A
    Premise

    3   ~B
        Premise

    4   ~A &amp; A
        Join, 1, 2

5   ~~B
    Conclusion, 3

6   B
    Rem DNeg, 5


7   A => B
    Conclusion, 2
8   ~A => [A => B]
    Conclusion, 1

score 0 · Answer 3 · answered Mar 08 '24 at 03:32

All fish are mammals (premise)
All mammals are animals that have gills (premise)
All fish are animals that have gills (conclusion)
Both premises are false, the argument is valid, the conclusion is true

All mammals are dogs (premise)
All dogs are zebras (premise)
All mammals are zebras (conclusion)
Both premises are false, the argument is valid, the conclusion is false

All dogs are mammals (premise)
All mammals are omnivores (premise)
All dogs are omnivores (conclusion)
One of the premises is false, the argument is valid, the conclusion is true

All dogs are mammals (premise)
All mammals are pink (premise)
All dogs are pink (conclusion)
One of the premises is false, the argument is valid, the conclusion is false

All fish are aquatic animals (premise)
All aquatic animals are animals that can swim (premise)
All animals that can swim are fish (conclusion)
True premises, invalid argument, false conclusion

All cats are mammals (premise)
All mammals are animals (premise)
Some animals are not cats (conclusion)
True premises, invalid argument, true conclusion

The only combo that is impossible is

True premises
Valid argument
False conclusion

Is it true that [if the premises are false, the conclusion is true]?

3 Answers3