0

I would like to know how to solve the limit of

$$\lim_{x\rightarrow\infty}e^{-t\sqrt{x}} \left(1 - \frac t{\sqrt x}\right)^{-x}$$

someone said the answer is $e^{t^2/2}$ but all I got is infinity.

Original Question

Consider a Gamma distribution with shape $\alpha$ and scale $\beta$, define variable $y$ in term of Gamma variable $x$ such that

$$y = \frac{x - \alpha\beta}{\sqrt{\alpha}\beta} = \frac{x}{\sqrt{\alpha}\beta} - \sqrt{\alpha}$$

Then MGF of $y$ is

$$M_y(t) = \mathbb{E}\left\{\exp\left(t(x/\sqrt{\alpha}\beta - \sqrt{\alpha})\right)\right\} = \exp(-t\sqrt{\alpha})\left(1 - \frac{t}{\sqrt{\alpha}}\right)^{-\alpha}$$

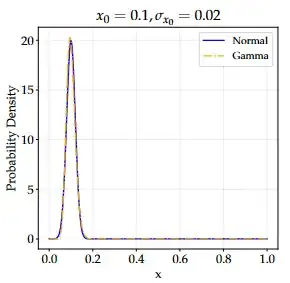
We know that the limit of Gamma is a Gaussian, see the figure, it follows that

$$\lim_{\alpha\rightarrow\infty}M_y(t)=e^{t^2/2}$$

I try to solve this limit simply by $\lim_{x\rightarrow\infty}(1 + 1/x)^x = e$, but still cannot get the right answer.

enter image description here

user170231
  • 19,334
Zuba Tupaki
  • 27
  • How did you get infinity? Please share your thinking (otherwise this will look like an attempt to outsource homework). Anyway, I would approach this limit by studying its logarithm. There may be a trick letting you do it without, but... – Jyrki Lahtonen Mar 06 '24 at 05:54
  • Oh, and you also need to add other context. Some solutions may rely on Taylor series expansion of $\ln(1+t)$. Are you familiar with that? – Jyrki Lahtonen Mar 06 '24 at 05:55
  • Thanks for the reminder, @JyrkiLahtonen, it is actually a proof showing the limit of Gamma distribution is a Gaussian. I will add my context later. – Zuba Tupaki Mar 06 '24 at 06:03
  • 1
    Also this. Apologies for neglecting to check for duplicates. Deleting the answer. – Jyrki Lahtonen Mar 06 '24 at 08:29

0 Answers0