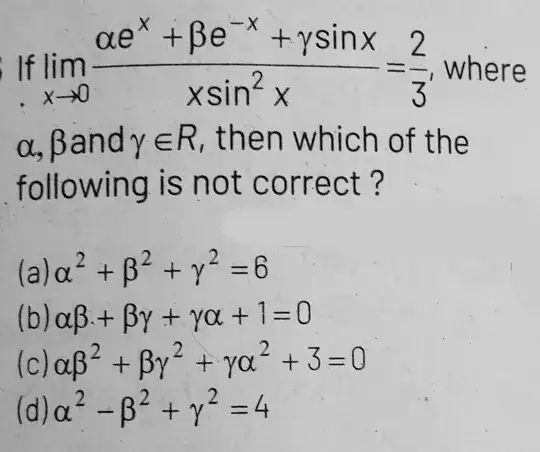 I couldn't solve this question so I looked for hints. One method of solving was to use the Taylor Series expansion of each of the functions.
It was a bit long.
So another solution used the L'Hospitals Rule instead.
I couldn't solve this question so I looked for hints. One method of solving was to use the Taylor Series expansion of each of the functions.
It was a bit long.
So another solution used the L'Hospitals Rule instead.
$$\lim_{x\to 0}{\cfrac{\alpha e^x+\beta e^{-x}+\gamma\sin(x)}{x\sin^2x}}$$
$$= \lim_{x\to 0}{\cfrac{\alpha e^x+\beta e^{-x}+\gamma\sin(x)}{x^3}}$$
For limit to be finite limit of numerator should be zero. Therefore $$\alpha +\beta =0.$$ But limit of $\sin x$ as $x$ tends to $0$ is taken as $x$ in most cases so the correct equation should be $$\alpha +\beta +\gamma x=0$$and further equations are obtained similarly.
Can the limit of $\sin x$ as $x$ tends to $0$ be taken as either $x$ or $0$ as per convenience?
Is using L'Hopitals Rule a correct method of solving this question?
OR Is Taylor series the more appropriate method?