Let $a>1$ be an integer. I wish to analyze the digits of the power sequence $(a^n)_n$. The behave of extreme digits can be settle to the following:
- The last $k$ digits of $a^n$ are given by $a^n\pmod{10^k}$, therefore the sequence of the $k$ last digits is eventually periodic and does not depend on subsequent digits.
- The first $k$ digits of $a^n$ are given by the number $s = \overline{(s_1s_2\dots s_k)}_{10}$ if, and only if, there is an integer $t$ such that $$\begin{alignat}{3} &10^t(s+1)& &>a^n& & &\ge 10^ts\\\iff &t+\log_{10}(s+1)& &>n\log_{10}(a)& & &\ge t+\log_{10}(s)\\\iff &\log_{10}(s+1)& &>\{n\log_{10}(a)\}~& & &\ge \log_{10}(s) \end{alignat}$$ Now the Equidistribution Theorem says that $(\{n\log_{10}(a)\})_n$ is equidistributed over $[0, 1]$ as long as $\log_{10}(a)$ is irrational (i.e., as long as $a$ is not a power of $10$), therefore $s$ occurs as the first set of digits of $a^n$ with probability $\log_{10}(s+1)-\log_{10}(s)$, or $\displaystyle\log_{10}\left(1+\frac1s\right)$. This not only says every string of digits occur as the first set of digits of $a^n$ for some $n$ but also says power sequences follows Benford's Law.
But what about the digits in between? The study of first and last digits require very specific tools which seem not easy to adapt or combine to adresse this particular case.
More precisely, I want to know the limit distribution of the digits which are not a fixed number of positions from the right or from the left of a power sequence. Is the sequence it periodic? Must every digit appear in it? What is the frequency of these digits?
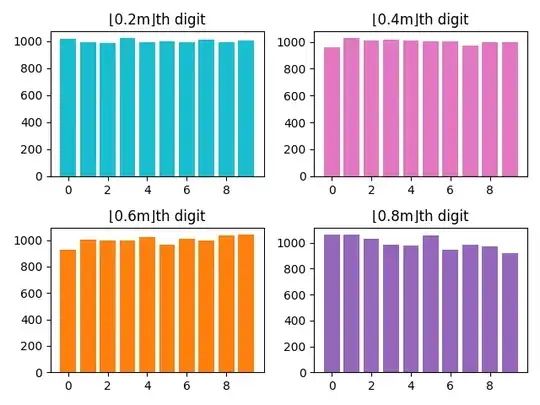
In an attempt to develop intuition I recurred to this Python script, which plots the frequency of each digit of $2^n$ in positions $\left\lfloor\dfrac 15m\right\rfloor, \left\lfloor\dfrac 25m\right\rfloor, \left\lfloor\dfrac 35m\right\rfloor, \left\lfloor\dfrac 45m\right\rfloor$, where $m$ is the total number of digits.
import numpy as np
import matplotlib.pyplot as plt
import sys
increases limit for integer-string conversion
sys.set_int_max_str_digits(0)
freq1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
freq2 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
freq3 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
freq4 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
a = 2 # power basis
for n in range(10000):
p = str(a*n) # power
m = len(p) # number of digits
freq1[int(p[int(0.2m)])]+=1
freq2[int(p[int(0.4*m)])]+=1
freq3[int(p[int(0.6*m)])]+=1
freq4[int(p[int(0.8*m)])]+=1
The code produces the following graphs.
The distribution seems to be approaching uniformity. The same behavior was observed for several other basis. This is my conjecture:
Conjecture. Given an integer $a>1$ not divisible by $10$, a digit $d$ and $\lambda\in(0,1)$, we have $$\lim\frac{\#(\{n:\text{ the }\lfloor\lambda m(a^n)\rfloor\text{th digit of }a^n\text{ is }d\}\cap[1, N])}{N} = \frac1{10}.$$ where $m(x)\equiv\lfloor\log_{10} x\rfloor$ is the amount of digits of $x$.
Of course, I have no reason to believe this only applies to base $10$.