On asymptotics of certain sums of multinomial coefficients

Question

Given positive integers $n$ and $k$, set $$ S_{n,k}=\sum_{\substack{a_1+a_2+\dots+a_k=2n\\ a_i \in 2\mathbb{N},\,i=1,\ldots,k}}\frac{(2n)!}{a_1!a_2!\dots a_k!}, $$ where $2\mathbb{N}=\{0,2,4,\ldots\}$. According to the answers of Special sum of multinomial coefficients! there is no "nice" closed form expression for $S_{n,k}$.

My question is: How can one find the asymptotics of $S_{n,k}$ for fixed $n$ when $k \rightarrow \infty$ ?

My thoughts so far: It is mentioned in the link above that the expression for $S_{n,k}$ resembles Sterling numbers of the second kind, so perhaps some approximation results for those numbers may be relevant. Also, I did some numerical experimentation that seems to suggest that the naive guess $S_{n,k}\sim C_n \cdot k^n$ (where $C_n>0$ depends on $n$ only) is plausible.

Answer 1

Let ${\bf X}$ be a $(2n,k)$ multinomial random variable, corresponding to the experiment of placing $2n$ balls inside $k$ urns, with uniform probability. Then

$$P_{\bf X} = \frac{(2n)!}{x_1!x_2! \cdots x_k!} (1/k)^{2n} \left[\sum x_i = 2n\right] \tag 1$$

Let $E$ be the event that all urns have an even number of balls. Then

$$k^{2n} \, P(E) = S_{n,k} \tag 2$$

If $k\to \infty$ and $n$ is fixed, then the probability that an urn gets more than two balls turns negligible, and we can just count the events that have $n$ urns with $2$ balls and the rest empty. Summing the probabilities of these events we get

$$S_{n,k} \approx \binom{k}{n}\frac{(2n)!}{2^n} \tag 3$$

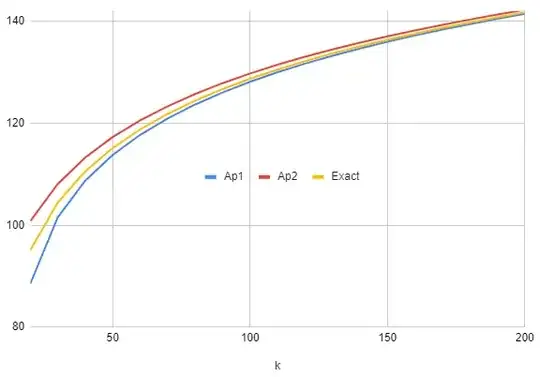
This approximation is similar to that of Mike Earnest, the graph displays $\log S_{n,k}$ for $n=18$ ("Ap1" is approx $(3)$, "Ap2" is Mike Earnest's)

It's also a lower bound, of course, because it omits some valid configurations.

Plugging in $(3)$ the Stirling approximation (first order) we get

$$S_{n,k} \approx (2 k n/e)^n$$

in agreement with your guess.

For both $n,k$ growing together, this approach (for Stirling numbers of the second kind) could be adapted.

---

Added: a really tight asymptotic, especially for large $k$ and $n$.

Let $m=2n$ and $\mu=m/k$, let $\lambda$ be the solution of $\lambda \tanh(\lambda) = \mu$ [*], and $\sigma^2=\lambda^2 + \mu(1-\mu)$

Then

$$S_{n,k} \approx \frac{ m! \, \cosh^k(\lambda)}{\lambda^{m}} \sqrt{\frac{2}{ \pi k \sigma^2}} \tag 4$$

This approximation (lets call it "Ap3") is based on the same approach given in the link above (kind of Poissonization), I can provide details if anyone is interested. It gives values that are practically indistinguishable from the exact values in the graph above.

Here's a table of values of $\log S_{n,k}$, for $n=18$.

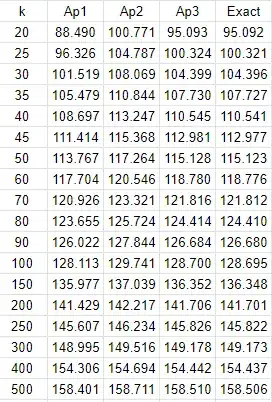
and for $n=5$

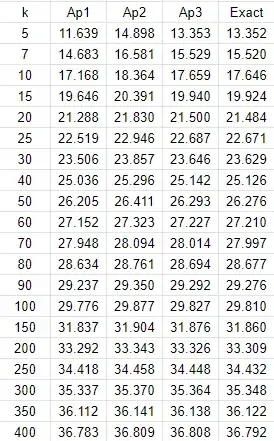
[*] To numerically find $\lambda$, one can start with $\lambda_0=\max(\mu,\sqrt{\mu})$ and iterate $\lambda_{i+1}=\sqrt{\mu \lambda_i/\tanh(\lambda_i)}$. It converges quite fast.

Answer 2

Claim: $S_{n,k}\sim (2n-1)!!\cdot k^n$ as $k\to\infty$, where $(2n-1)!!=(2n-1)(2n-3)\cdots 3\cdot 1.$

Proof: Let $\Omega$ be the set of sequences of length $2n$ where each entry is in $\{1,\dots,k\}$, so $|\Omega|=k^{2n}$. Let $\newcommand{\oe}{\Omega_\text{even}}\oe$ be the set of sequences $\omega\in \Omega$ such that, for each $i\in \{1,\dots,k\}$, the number $i$ appears an even number of times in $\omega$. Then $$ |\oe|=S_{n,k} $$ Indeed, given a list $(a_1,\dots,a_k)$, the number of sequences where $i$ appears $a_i$ for each $i\in k$ is $\frac{(2n)!}{(a_1)!\cdots (a_k)!}$, so you conclude by summing over all lists where each $a_i\in 2\mathbb N$ and $a_1+\dots+a_k=2n$.

Each $\omega$ in $\oe$ determines a partition of $\{1,\dots,2n\}$ where all parts have even cardinality. For each $i$ which appears in $\omega$, one of the parts of this partition is the set of $j\in \{1,\dots,2n\}$ such that $\omega_j=i$. Conversely, given a partition of $\{1,\dots,2n\}$ where all parts are even, and there are $p$ parts, the number of $\omega$ which correspond to that partition is $$ k\cdot (k-1)\cdots (k-p+1)=\frac{k!}{(k-p)!}\sim k^p $$ This is because there are $k$ ways to fill the spots in the first part, then $(k-1)$ ways to fill the spots in the second part with a different number, and so on.

Now, we can write $|\oe|$ as the sum over all even partitions of $\{1,\dots,2n\}$ of the number of sequences which generate that partition. The number of partitions is constant with respect to $k$, and we see that each partition with $p$ parts gives a term with a growth rate of $k^p$. Since the maximum value of $p$ is $n$, which occurs when there are $n$ parts of size $2$, this implies that the growth rate of $|\oe|$ is equal to $k^n$ times the number of partitions of $\{1,\dots,2n\}$ into $n$ parts of size $2$. It is well known that that the number of such partitions is $(2n-1)!!$, completing the proof. $\tag*{$\square$}$

Effective bounds

Using the same argument, you can more specifically show that $$ (2n-1)!!\cdot \frac{k!}{(k-n)!} \le S_{n,k} \le (2n-1)!!\frac{k!}{(k-n)!}+C_n\cdot \frac{k!}{(k-n+1)!} $$ where $C_n$ is the number of partitions of $\{1,\dots,2n\}$, such that each part is even, and such that there are at most $n-1$ parts. For the lower bound, we are only considering partitions with $n$ parts of size $2$. For the upper bound, we consider all partitions, but for each partition with $p\le n-1$ parts, we upper bound the summand of $k!/(k-p)!$ by $k!/(k-n+1)!$.

If we write $\newcommand{\fall}[2]{#1^{\,\underline{#2}}}k!/(k-n)!=\fall kn$ (this is Knuth's notation for the falling facotiral), then we can write this a little nicer: $$ (2n-1)!!\cdot \fall kn \le S_{n,k} \le (2n-1)!!\cdot \fall kn+C_n\cdot \fall k{n-1} $$ Note that $\fall kn \sim k^n$ as $k\to\infty$.