On the "efficiency" of digit-sum divisibility tricks in other bases (or about the growth rate of the number of divisors function).

Question

Out of the different divisibility tricks there's a really simple rule that works for more than one divisor: The digit-sum. Specifically, if the sum of the digits of a number is a multiple of $1,3$ or $9$ then so was the original number (although the $1$ case is trivial it'll make sense to include it for later).

One can then ask: On how many different numbers does the divisibility trick work if we consider different bases besides $10$? To answer the question, we recall that the digit-sum works in base $10$ for $1,3$ and $9$ because if we have some $n$-digit number $x= \sum_{k=0}^{n} 10^k a_k$ with digits $a_k \in \mathbb{N}\cap[0,\dots,9]$ then we can write $$ x = \sum_{k=0}^{n} 10^k a_k = \sum_{k=0}^{n}\left( 10^k+1-1 \right)a_k = \sum_{k=0}^{n}\left(10^k-1\right)+ \underbrace{\sum_{k=0}^{n}a_k}_{\color{purple}{\text{Sum of digits}}} $$ so we just need to find when $10 \equiv 1 \pmod{x}$ since these $x$'s will make $ \sum_{k=0}^{n}\left(10^k-1\right)\equiv 0 \pmod{x}$ and thus giving us a working digit-sum divisibility rule. But asking $10 \equiv 1 \pmod{x}$ is just asking the number of $x$'s that satisfy $x \vert 10-1$, which is exactly the number of divisors of $10-1 =9$.

Repeating this procedure for a general base $b$ we obtain that the number of working divisibility tricks in a base $b$ is just $\sigma_0(b-1)$, where $\sigma_0(z)$ is the number of divisors function. This then motivates a definition for how "efficient" a base is at having multiple digit-sum divisibility tricks as follows: $$ E(b) = \frac{\sigma_0(b-1)}{b-1}, \quad b \in \mathbb{N}\cap[2,\infty) $$ In this way, $E(b)$ represents the percentage of working digit sum tricks out of all possible numbers less than $b$ when written in base $b$.

For the base $b=10$ we have $E(10) = \frac{\color{purple}{3}}{\color{green}{9}}$ since we get $\color{purple}{3}$ working digit-sum tricks (for $1,3$ and $9$) out of the $\color{green}{9}$ possibilities $1,2,\dots,9$.

On the other hand, for the base $b=15$ we have $E(15) = \frac{4}{14}$ with the four digits with digit-sum rules being $1,2,7$ and $14$. So for example $4389_{10}$ in base $15$ is $1479_{15}$ and since $ 1+4+7+9 = 21$ is divisible by $7$, then so is $1479_{15}=4389_{10}$.

---

My main question is the following:

What can we say about the behavior of $E(b)$?

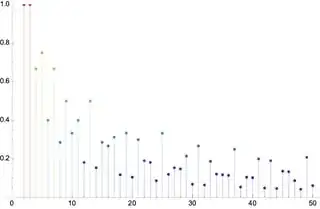
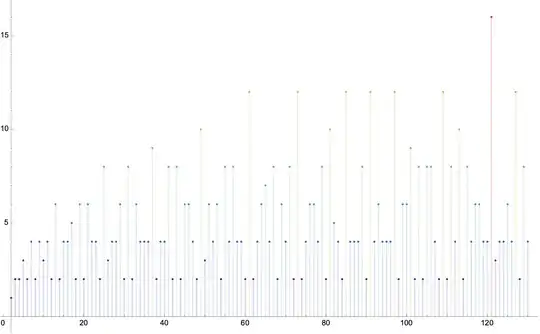
For example, when graphing $E(b)$ you get the following:

We can see that bases $2$ and $3$ have a $100$% digit-sum trick effectiveness, meaning that the digit-sum trick works for all numbers less than their respective bases.

Another thing to notice is that we occasionally get spikes in the graph. Some of these can be attributed to highly composite numbers which are numbers $n$ that satisfy $\sigma_0(n) \ge \sigma_0(k)$ for all $k \le n$. The spike on $E(25)$ is because $24$ is a highly composite number, and the spike at $E(13)$ is because $12$ is a highly composite number. Thus, if you pick a base one more than a highly composite number you'll get several working digit-sum divisibility tricks.

We can also explain most "dips" in the graph for a similar reason. Since $\sigma_0(p) =2$ for any prime $p$, then for bases one more than a prime you'll get efficiency $E(p+1) = \frac{2}{p}$ which can get arbitrarily small for larger and larger primes.

Some other example questions might be:

• What are some upper/lower bounds on $E(b)$?
• How fast does $E(b)$ decrease?
• How often do we get spikes in the graph of $E(b)$?

Any and all ideas are very much welcome. Thank you for reading!

Answer 1

Following up on the observation by @Eric Snyder, we can explicitly show some subsets of $\mathbb{N}$ that have the same evaluation of $\sigma_0(n)$. First, we recall that if $n= \prod_{i=1}^{r}p_i^{a_i}$ is $n$'s prime factorization (which means all $p_i$ are prime and all $a_i >0$) then $\sigma_0(n) = \prod_{i=1}^{r} (a_i+1)$.

• $\sigma_0(n) =q$ for some prime $q$ $\iff$ $n =p^{q-1}$ for $p,q$ primes.

Proof: The reverse implication is immediate just by substituting $\sigma_0(p^{q-1}) = (q-1+1)=q$. For the forwards implication, since $\sigma_0(n) =q$ then $(a_1+1) \vert q$. Since $q$ is prime then $a_1 +1 \in \{1,q\}$, but since $a_1 \neq 0$ then the only option is that $a_1 =q-1$. Lastly, if we were to have some other $a_2 >0$ in the factorization of $n$ then $\sigma_0(n) =\prod_{i=1}^{r} (a_i+1)\ge q(a_2+1) > q$ which is a contradiction since we're assuming that $\sigma_0(n) =q$. Thus $n =p^{q-1}$ for some primes $p,q$. $\ \blacksquare$

This allows us to explicitly write some families of solutions, which includes Eric's example for $3$: $$ E(b) = \frac{3}{b-1} \iff \sigma_{0}(b-1) = 3 \iff b \in \left\{n \in \mathbb{N} \, \vert \, n=p^2+1,\, p \text{ prime} \right\} = \{5,10,26,50,\dots\} $$ So we indeed have an infinite number of subsets of $\mathbb{N}$ that trace hyperbolas and we can explicitly list them, one for each prime.

Here's a graph of just $\sigma_0(b-1)$: