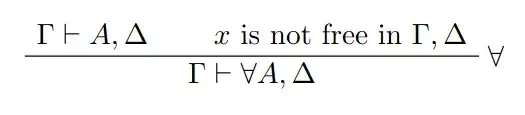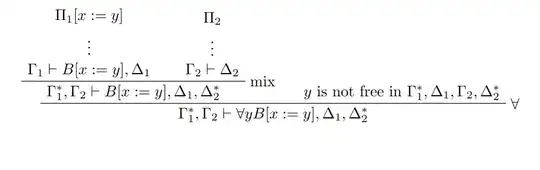3

Lately I have been reading about the cut elimination theorem, I think I get the idea however I have been struggling with some technical details concerning quantifiers.

Consider the following rule:

enter image description here

Now in the proof of the cut elimination theorem we are using mixes instead of cuts for technical reasons, so if it appears in a mix (but is inactive) in the following way:

enter image description here

In the above at the "mix" step the idea is that we remove some occurrences of a formula $A$ from $\Gamma_1$ and $\Delta_2$ to get $\Gamma_1^*$ and $\Delta_2^*$. We can find $y$ a variable that appears nowhere and reformulate this step to find:

enter image description here

Now we can use induction to see that we can eliminate the cut, this seems good. However, in the conclusion we end up with $\forall y B[x:=y]$ instead of $\forall x B$ this may not seem to be a big deal because we can go from one formula to the other by doing a substitution... But formally this does not seem to be fine because if I were to go from $\Gamma_1^*, \Gamma_2 \vdash \forall y B[x := y], \Delta_1, \Delta_2^*$ to $\Gamma_1^*, \Gamma_2 \vdash \forall x B, \Delta_1, \Delta_2^*$ I would use $\forall y B[x := y] \vdash \forall x B$ and a cut which would break everything since I can not use the induction anymore to get rid of the cut since the length of the proof will be too long.

Is it possible to end up with $\forall x B$ instead of $\forall y B[x := y]$ without breaking the induction?

Taroccoesbrocco
  • 16,964
Le Grand Spectacle
  • 253

1 Answers1

3

The short answer is: the formula $\forall x B$ is identical to the formula $\forall y B[x:= y]$. Indeed, in a proof-theoretical context, for technical reasons to avoid dealing with annoying syntactical details, first-order formulas are considered as identified up to the renaming of bound variables, where a variable is bound if it is under the scope of a universal or existential quantifier.

For instance, if $P$ is an unary predicate symbol, $\forall x P(x) = \forall y P(y)$. Said differently, in proof theory for first-order logic, bound variables are dummy in that they appear in a formula only as a placeholder and they can be changed without modifying the meaning of the formula (see also here and here).

(This is analogous to what happens in mathematical analysis, where the integrals $\int_a^b f(x) dx$ and $\int_a^b f(y) dy$ are the same thing.)

As a consequence, the sequents $\Gamma_1^*, \Gamma_2 \vdash \forall x B, \Delta_1, \Delta_2^*$ and $\Gamma_1^*, \Gamma_2 \vdash \forall y B[x:= y], \Delta_1, \Delta_2^*$ are the same, hence the argument to prove the cut-elimination theorem is correct in this respect, and you can safely use the induction hypothesis without the need for any further manipulations.

Taroccoesbrocco
  • 16,964
  • I at least am not used to the convention of identifying first-order formulas up to renaming of bound variables, and I certainly wouldn't say that the two formulas in question are identical. – Noah Schweber Feb 26 '24 at 20:22
  • @NoahSchweber - For you, $\forall x , x = x$ and $\forall y , y = y$ are not the same formula? If you don't identify formulas up to the renaming of bound variables, how can you correctly define the notion of substitution (which is crucial for instance, for the inference rules concerning quantifiers in the sequent calculus) to avoid the capture of variables? – Taroccoesbrocco Feb 26 '24 at 20:32
  • 1
    @NoahSchweber - I'm perfectly aware that defining the quotient on the set of formulas to identify them up to the renaming of bound variables is annoying. In a model-theoretic context, there is no point in doing that, so it makes sense to consider formulas without any quotient (we can say that $∀, =$ and $∀, =$ are just distinct logically equivalent). But in a proof-theoretic context, as in the OP, identifying formulas up to the renaming of bound formulas is crucial and standard, unless you want to deal with even more syntactic and annoying details. – Taroccoesbrocco Feb 26 '24 at 20:39
  • Yes, I don't view $\forall x(x=x)$ and $\forall y (y=y)$ as the same formula; they are genuinely different strings of symbols. I don't see the issue with substitution; you just have to be a bit careful how you define things. I didn't know that this was the standard style in proof theory, though, so I'll remove my downvote. (EDIT: apparently I can't because too much time has passed; if you edit this, I'll remove the downvote.) – Noah Schweber Feb 26 '24 at 20:47
  • @NoahSchweber - Done. Anyway, thank you for the discussion, there is always something to learn when seeing the same thing from different viewpoints. – Taroccoesbrocco Feb 26 '24 at 20:57
  • 1
    There would also be the option of using de Bruijn indices in the lowest-level encoding of formulas -- in that case, $\forall x (x = x)$ and $\forall y (y = y)$ would be two versions of syntactic sugar for the same underlying object $\forall {\cdot} ([0] = [0])$. – Daniel Schepler Feb 28 '24 at 00:31
  • Thank you all for these explanations. As I am not a logician I was not sure if this identification was acceptable. But a natural follow up question I would ask is that if I do not identify $B$ with $\forall y B[x:=y]$, is the cut elimination theorem still true? – Le Grand Spectacle Mar 01 '24 at 13:36
  • @LeGrandSpectacle - A short answer is: yes, up to renaming bound variables! I mean, you can always say that the conclusion sequent you have after a cut-elimination step is obtained from the conclusion sequent before the step by renaming its bound variables. If you want to define cut-elimination to preserve the same sequent without identifying formulas up to renaming bound variables, I would say that probably you can do it (even though I never saw a proof of it), but I'm not sure, and it should be very tricky and annoying to prove, because of many syntactic nuisances. – Taroccoesbrocco Mar 01 '24 at 17:48
  • @LeGrandSpectacle - Pay attention that in your last comment you talk about identifying $B$ and $\forall y B[x:=y]$, but this is not what I meant. When I talk about renaming bound variables, I mean to identify formulas like $\forall x B$ and $\forall y B[x:=y]$. – Taroccoesbrocco Mar 01 '24 at 17:50
  • @Taroccoesbrocco Yes indeed I ment to identify $\forall x B$ and $\forall y B[x:=y]$. – Le Grand Spectacle Mar 01 '24 at 23:22
  • I did try to prove the cut elimination theorem by trying to preserve the same end sequent without identification but I was not successful in doing so. As you said, many syntactic nuisances come into play... – Le Grand Spectacle Mar 01 '24 at 23:24