Can Markov Chains be used to Disprove the St Petersburg Paradox?

Question

I am learning about the St Petersburg Paradox https://en.wikipedia.org/wiki/St._Petersburg_paradox - here is my attempt to summarize it:

• A fair coin is tossed at each stage.
• The initial stake begins at 2 dollars and is doubled every time tails appears.
• The first time heads appears, the game ends and the player wins whatever is the current stake

As we can see, this game will have an expected reward of infinite dollars:

$$E(X) = \sum_{i=1}^{\infty} x_i \cdot p_i$$

$$E = \sum_{n=1}^{\infty} \frac{1}{2^n} \cdot 2^n = \frac{1}{2} \cdot 2 + \frac{1}{4} \cdot 4 + \frac{1}{8} \cdot 8 + \frac{1}{16} \cdot 16 + ... = 1 + 1 + 1 + 1 + ... = \sum_{n=1}^{\infty} 1 = \infty$$

The paradox is that even though the game has an infinite reward, in real life simulations, the game usually ends up with a finite reward. Although seemingly counterintuitive, this does seem logical. Even more, we can write computer simulations to see that large number of games will have finite rewards.

I had the following thought: Using the theory of Absorbing Markov Chains (https://en.wikipedia.org/wiki/Absorbing_Markov_chain), we can find out how many trials it takes for the first head to appear:

$$ P = \begin{bmatrix} p_{TT} & p_{TH} \\ p_{HT} & p_{HH} \end{bmatrix} = \begin{bmatrix} 1/2 & 1/2 \\ 0 & 1 \end{bmatrix} $$

where:

• $p_{HH}$ is the probability of going from state "H" to state "H"
• $p_{HT}$ is the probability of going from state "H" to state "T"
• $p_{TH}$ is the probability of going from state "T" to state "H"
• $p_{TT}$ is the probability of going from state "T" to state "T"

The fundamental matrix $N$ is defined as $N = (I - Q)^{-1}$, where $I$ is the identity matrix and $Q$ is the submatrix of $P$ containing only the transient states. In this case, $Q$ is a 1x1 matrix containing the single entry 1/2, so:

$$ Q = \begin{bmatrix} 1/2 \end{bmatrix} $$ $$ I = \begin{bmatrix} 1 \end{bmatrix} $$

Therefore,

$$ N = (I - Q)^{-1} = \left( \begin{bmatrix} 1 \end{bmatrix} - \begin{bmatrix} 1/2 \end{bmatrix} \right)^{-1} = \begin{bmatrix} 2 \end{bmatrix} $$

The same result can be directly obtained from taking the Expected Value of the Geometric Distribution, if we define the first heads (ironically) as the the first success:

$$ P(X=k) = (1-p)^{k-1}p $$

$$ E[X] = \frac{1}{p} $$

From here, its clear to see that when $p=0.5$, then $E[x] = 2$.

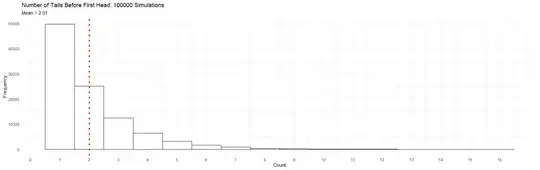
I then wrote this simulation in R to confirm the results (i.e. coin flipping simulations):

   flip_until_head <- function() {
    count = 1
    while(sample(c("H", "T"), 1) == "T") {
        count = count + 1
    }
    return(count)
}
results <- replicate(100000, flip_until_head())
mean_count <- mean(results)
ggplot(data.frame(results), aes(x=results)) +
    geom_histogram(binwidth=1, color="black", fill="white") +
    geom_vline(aes(xintercept=mean_count), color="red", linetype="dotted", size=1.5) +
    labs(title="Number of Tails Before First Head: 100000 Simulations",
         subtitle=paste("Mean =", round(mean_count, 2)),
         x="Count", y="Frequency") +
    scale_x_continuous(breaks = 0:max(results)) +
    theme_minimal()

I conclude with the following thoughts:

• Through Markov Chains and the Geometric Distribution it is unreasonable to believe that the game being played within the St Petersburg Paradox will last forever. There is a finite time to absorption (i.e. end of game).
• Since there is a finite number of turns in which the game is expected to end, there is a finite reward in this game
• Therefore, from the perspective of Absorbing Markov Chains, it appears that the St Petersburg Paradox is not really a paradox : It is a game with finite duration and finite reward.
• But from the perspective of the classical expectation analysis, the game will have an infinite reward

Is this analysis correct?

Answer 1

I think the final interpretation you have given of the math you have done is not correct, which is not to say there's anything wrong with the code or calculations. The expectation of earnings in the St. Petersburg "paradox" is infinite (as the original analysis proves) even though the expected number of flips is finite. That is not a contradiction.

There is no way to use some new mathematical technology or language to disprove that the expectation is infinite, so nothing is resolved.

In my opinion there is nothing paradoxical in the St. Petersburg paradox to resolve in the first place. It just goes to show that in risk analysis, knowing the expectation of a distribution is insufficient for rational decision-making.