7

In "Power-law Distributions in Empirical Data", the authors give several examples of alleged power-laws. For instance, they plot node degree distribution of the Internet like this (p. 24):

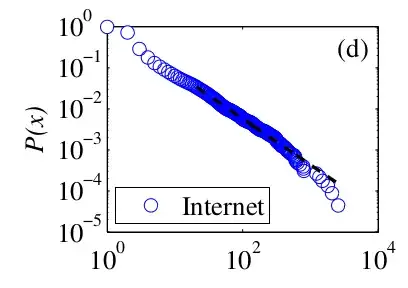
enter image description here

where $P(x)$ is the cumulative distribution function and the black dashed line is the power-law fit, starting from some $x_{\text{min}}$.

As far as I understand, $P(x)$ is calculated as

$$ P(x) = \frac{|\{v : v \in V \wedge \text{degree}(v) > x\}|}{|V|} $$

i.e. the fraction of nodes that have degree higher than $x$.

According to Wikipedia, plotting the cumulative distribution is common when plotting power laws. However, if I want to plot my power-law fit as well in the same chart, what do I plot? I do have an exponent $k$ that I understand to mean that the frequencies of degrees follow a power law $y \propto x^{-k}$. How do I derive a function from this that can be displayed in the cumulative distribution plot like the dashed power-law fit in the example plot above?

notan3xit
  • 171
  • 1
  • 4

1 Answers1

3

The blue dots represent the complementary cumulative distribution function (abbreviated "ccdf"), which is, as you say, defined as the fraction of the vertices with degree at least $k$. The range of $k$ here is in principle any natural number, but the creators of the figure have observed that the ccdf is constant at values of $k$ that don't appear in the data, so instead they have omitted those points for clarity. Let's define this empirical ccdf as $F(k)$.

The fitted power-law distribution (shown in the figure as the black dashed line) requires two parameters $\alpha$ and $k_{\min}$. If we assume those are known (or have been estimated properly), then the ccdf of the power law has the form $P(k) = (k/k_{\min})^{-\alpha+1}$. This equation is something you can verify for yourself, by evaluating the integral $\int_k^\infty p(x){\rm d}x$ with $p(x)$ as the normalized pdf for the power law. Note that $P(k=1)=1$, representing the fact that all vertices have degree at least 1.

The one tricky thing the creators of the figure did was to vertically shift the fitted power law so that it lines up with the data, starting at the empirical ccdf value for $k_\min$. That is, they plotted $F(k_\min)\times (k/k_{\min})^{-\alpha+1}$.

aaronclauset
  • 131