Given an n-digit integer sequence, e.g. $n=5$ [1, 1, 5, 6, 4] where each digit is independent and uniformly random in the range 1-6, what is the probability of having at least k same digits of a certain value (e.g. 1)?
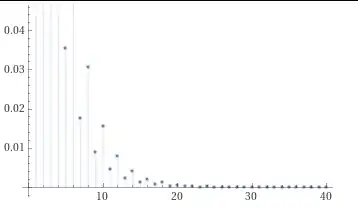
Specifically I'm interested in $k = n/2$ (rounded up) and n in the range 1 - 40.
So ... f(k, n) = Probability of *at least* k same of a specific digit = ... n ... k ...?
Background:
This is as far as I got with the question of plotting the probability of rolling $n$ dice once and having at least $k$ 1s in the resulting roll. (e.g. at least half the dice showing 1.)
Yes, there are $6^n$ combinations to roll $n$ dice. The probability for each die to show or not show a 1 is $1/6$ or $5/6$ respectively.
Yes, the question is the same whether asking if we have at least half 1s or at least half 4s ... any single digit, the others are irrelevant. And, yes, it does not matter if I roll $n$ dice once to generate the sequence or one die $n$ times.
That it is $1/6$ for one die is trivial. For two dice I can come up with a calculation, and is still easy to check with a table - $11/36$), but I fail to come up with a calculable general solution for $n >= 3$
Similar to this other question I'm currently looking at the binomial distribution but I'm stuck a bit at the moment.
Side Side Note: The question for increasing n comes from a discussion we had on if, and how much, the probability of rolling more than half 1s with a hand full of D6 dice increases with the number of dice.