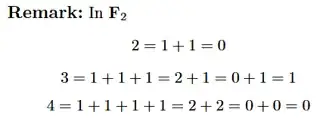What are $0$ and $1$, the elements of $\mathbb Z/2\mathbb Z$? How do they relate to $\mathbb Z$?

Question

I often see field $\mathbf{Z}/\mathbf{2Z}=\{0,1\}$. Without other indication we might see elements of field $\mathbf{Z}/\mathbf{2Z}$ as a subset of $\mathbf{Z}$. Operations such as $2+1=3=1$ are also given as examples:

Source.

I understand this field is the one defining the sum modulo-2 (and the Boolean addition provided we associate False/True to $0$/$1$), and in $\mathbf {Z}$, $3$ modulo $2= 1$ but I've some difficulty to fully understand these statements:

$2+1=3=1$ seems incorrect since the addition associated with field $\mathbf{Z}/\mathbf{2Z}$ (the modulo/boolean addition) is used on elements $2$ and $1$, but $2$ is not in $\mathbf{Z}/\mathbf{2Z}$.
$3=1$ seems to be used (approximately) to indicate there is a correspondence between $3 \in \mathbf {Z}$ and $1 \in \mathbf {Z} / \mathbf {2Z}$.

On the other hand, my understanding is elements of field $\mathbf{Z}/\mathbf{2Z}$, denoted $0$ and $1$ are actually classes of elements of group $\mathbf{Z}$:

$2+1$ should rather be written $0 + 1 = 1$, as $0$ (of $\mathbf{Z} / \mathbf{2Z}$) is the class corresponding to number $2$ (of $\mathbf{Z}$), and $1$ is the class corresponding to number $1$.

Can someone provide a rigorous explanation with a more accurate wording on what is the field $\mathbf{Z}/\mathbf{2Z}$, how is is related to $\mathbf{Z}$ and what is the nature of its elements?

The elements are residue classes. Basically, $\overline{0}$ is the set of all even integers, and $\overline{1}$ is the set of all odd integers. — Jyrki Lahtonen, Feb 14 '24 at 10:05
Wikipedia on modular arithmetic may be the best WP source. Here it is (in my opinion) either off topic, or duplicate zillion times over. — Jyrki Lahtonen, Feb 14 '24 at 10:07
Also this wikipedia article for the field with $2$ elements. — Dietrich Burde, Feb 14 '24 at 10:28
The correct setting to talk rigorously about $\mathbb{Z} /2\mathbb{Z} $ is that of quotient rings. Intuitively it's the same thing as quotient vector spaces but with other operations to be preserved. Namely in your case you have a ring structure on $\mathbb{Z}$ and you take the quotient classes modulo $2\mathbb{Z}$ (you can see that the set of quotient classes has a natural ring structure with the operation induced by the ring structure of $\mathbb{Z}$. (not posting this as an answer because this is just to give an idea. If someone wants to espand, feel free to do it) — Temoi, Feb 14 '24 at 11:37
As explained here in the linked dupe, it arises by transporting the qutient ring structures to remainder reps of the cosets, i.e. we rep $,a+(n)\in \Bbb Z/(n),$ by the remainder $,\ a\bmod n (= $ least nonnegative elt of the coset). — Bill Dubuque, Feb 14 '24 at 13:27

J.Dmaths · Answer 1 · 2024-02-14T14:52:57.313

1

$\mathbf{Z}/\mathbf{2Z}$ is a field represented by the two equivalence classes of integers modulo 2. We take ${0},{1}$ as representatives of the two classes given by the partition which splits the integers between even and odd, where 0 is in the class of all even integers, 1 is in the class of all odd integers.

Then, you can check , that addition and multiplication are well-defined (which they are), and that it satisfies all the field axioms. As you said , Edit: Credit to Mark S below "2 is not in that set, but the equivalence class modulo 2, [2]=[0] is in that set" , which is what $\mathbf{Z}/\mathbf{2Z}$ represents: equivalence classes under mod 2.

edited Feb 14 '24 at 14:52

answered Feb 14 '24 at 10:18

J.Dmaths

715

1

Thanks, that confirms my view. I was confused by $2+1=1$, with a left side in Z, and a right side in Z/2Z. The right side should be $=3 (mod 2)$ which is also in Z (or both sides should be in Z/2Z). While the meaning is clear for seasoned mathematicians who do the mapping, it's confusing for learners. – mins Feb 14 '24 at 11:06
@mins Personally, I would prefer to say something like "2 means 1+1 in whatever system in question we're looking at. So in $\mathbb Z/2\mathbb Z$, $2+1=1$ is true and involves no integers, but instead means that $(1+1)+1=1$." – Mark S. Feb 14 '24 at 12:41
@J.Dmaths, I feel your writing of $2(mod2)\equiv0$ mixes together the operator usage (common in computer science) and the relation usage (more common in math) of "mod" in a way I find confusing and likely in conflict with what mathematicians intend. – Mark S. Feb 14 '24 at 12:44
How should I edit it to make it clearer? @MarkS. – J.Dmaths Feb 14 '24 at 12:51
@MarkS.: "in $\mathbb{Z} / \mathbb{2Z}$, $2+1=1$ is true". I'm confused by the fact the operator associated with $\mathbb{Z} / \mathbb{2Z}$ is used on elements which don't belong to $\mathbb{Z} / \mathbb{2Z}$ (2 is not in $\mathbb {Z} / \mathbb {2Z}$). I may be wrong, and that's the whole point of my question, but this operator is not defined for 2+1. – mins Feb 14 '24 at 12:51
@mins I am disagreeing with your assumption that the symbol "2" (or "1", for that matter) can refer only to the integer 2. Rather, these are context-dependent symbols. For instance, as documented at the Wikipedia page for identity, "1" is often used for the multiplicative identity, no matter what context (e.g. which ring) we are in. Similarly, in a context where the multiplicative identity can be added to itself, "2" denotes "1+1" where addition and the identity "1" are determined from context (e.g. the standard ones in Z/2Z). – Mark S. Feb 14 '24 at 14:12
@J.Dmaths It depends what precisely you would like to convey. For instance, you could write something like "2 is not in that set, but the equivalence class modulo 2, [2]=[0] is in that set". I might still argue with you on that point, but that phrasing would at least be clear and in line with mathematical usage. – Mark S. Feb 14 '24 at 14:15
Ah, ok I understand what you mean now about the notation : Yes , that part is slightly confusing , I will edit it to how you have said! – J.Dmaths Feb 14 '24 at 14:52

What are $0$ and $1$, the elements of $\mathbb Z/2\mathbb Z$? How do they relate to $\mathbb Z$?

1 Answers1