First of all, as you correctly say, the integrand $f(x) =\frac{x^2}{x^2+x-2}$ has vertical asymptotes at $x=-2$ and at $x=1$. This means that its domain is not, as you seem to think, the entire number line, but rather the number line with $-2$ and $1$ removed, i.e. $(-\infty,-2)\cup(-2,1)\cup(1,\infty)$.
Then, you do not distinguish clearly enough between the indefinite integral
$$\int \frac{x^2}{x^2+x-2} dx$$
and a definite integral (with one fixed bound $a$ and one moving boundary $x$) of the form
$$F_a(x) = \int_a^x \frac{t^2}{t^2+t-2} dt$$
The indefinite integral
$$\int \frac{x^2}{x^2+x-2} dx$$
is a purely symbolic notation which asks for the most general form of all antiderivatives of $f(x) =\frac{x^2}{x^2+x-2}$ on its domain (it cannot have an antiderivative outside of its domain), which as said earlier is $(-\infty,-2)\cup(-2,1)\cup(1,\infty)$. The correct answer to that would actually be
$$\int \frac{x^2}{x^2+x-2} dx = \begin{cases} x-\frac{4}{3} \ln\lvert 2+x \rvert+\frac{1}{3}\ln\lvert x-1\rvert +C \text{ if } x \in (-\infty,-2) \\ x-\frac{4}{3} \ln\lvert 2+x \rvert+\frac{1}{3}\ln\lvert x-1\rvert +D \text{ if } x \in (-2,1) \\ x-\frac{4}{3} \ln\lvert 2+x \rvert+\frac{1}{3}\ln\lvert x-1\rvert +E \text{ if } x \in (1,\infty) \end{cases}$$
where $C, D, E$ can be any real numbers, independently of each other. Even good textbooks forget about this subtlety, that the constant can be chosen differently on each connected component of the domain, and would write as answer just
$$x-\frac{4}{3} \ln\lvert 2+x \rvert+\frac{1}{3}\ln\lvert x-1\rvert +C.$$
They should, however, always include the absolute values in the logarithms. Written without them, the whole thing only makes sense for $x > 1$ because otherwise $\ln(x-1)$ is not defined. By the way, the more precise version actually comes in handy if one does not like absolute values, as on each part of the domain the sign of each term is clear:
$$\int \frac{x^2}{x^2+x-2} dx = \begin{cases} x-\frac{4}{3} \ln (-x-2) +\frac{1}{3}\ln (1-x) +C \text{ if } x \in (-\infty,-2) \\ x-\frac{4}{3} \ln (2+x)+\frac{1}{3}\ln (1-x)+D \text{ if } x \in (-2,1) \\ x-\frac{4}{3} \ln (2+x) +\frac{1}{3}\ln (x-1) +E \text{ if } x \in (1,\infty). \end{cases}$$
Now what about a function of the form
$$F_a(x) = \int_a^x \frac{t^2}{t^2+t-2} dt$$
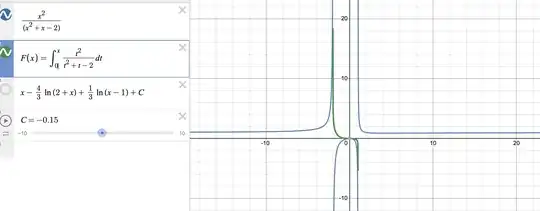
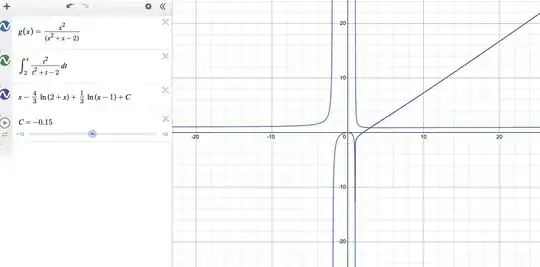
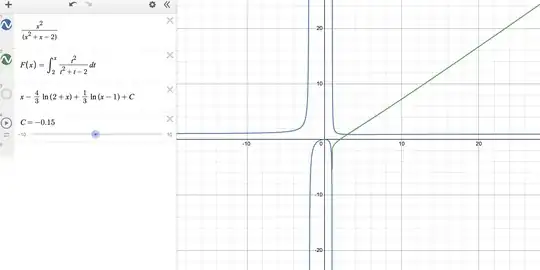
that you asked Desmos to plot there? Well the Fundamental Theorem says that this is one specific antiderivative of $f$ for $x\in [a,b]$ (or $[b,a]$) as long as $f$ is continuous on all of $[a,b]$ (or $[b,a]$). But as you say yourself, $f$ does have two rather bad discontinuities, at $-1$ and at $2$. As soon as either of them lies between $a$ and $x$, the integral defining $F_a(x)$ simply does not exist. What that means is that
For $a <-1$, the function $F_a(x) = \int_a^x \frac{t^2}{t^2+t-2} dt$ has domain $(-\infty, -1)$, and on that interval is an antiderivative of $f$.
For $-1<a<2$, the function $F_a(x) = \int_a^x \frac{t^2}{t^2+t-2} dt$ has domain $(-1, 2)$, and on that interval is an antiderivative of $f$.
For $2<a$, the function $F_a(x) = \int_a^x \frac{t^2}{t^2+t-2} dt$ has domain $(2, \infty)$, and on that interval is an antiderivative of $f$.
In either case, the function (on the corresponding interval and only there) must again be of the form $F_a(x)=x-\frac{4}{3} \ln\lvert 2+x \rvert+\frac{1}{3}\ln\lvert x-1\rvert +C$, but for a specific $C$ depending on $a$: where $C$ is to be computed easily from $F_a(a)=0$. And if you look closely, that is what Desmos plots for you in each case.
Added in response to the added question, "When integrating rational functions is this a common occurrence": Of course, analogous results hold for any function whose domain is all of $\mathbb R$ except for a discrete (e.g. finite) set of points, and which is continuous on said domain. That includes every rational function $\dfrac{p(x)}{q(x)}$, where that set is the finite set of solutions to $q(x)=0$ -- as soon as $q$ has any zeroes, the function has discontinuities. But similar things hold e.g. for $\tan(x) = \dfrac{\sin(x)}{\cos(x)}$ etc. The basic case $\displaystyle \int \dfrac{1}{x} dx$ is addressed e.g. in this question or in this video.