So recently I was thinking about solving definite integrals forms of: $$\int_{ka}^{kb} f(x) dx$$ and rearrange this as: $$\int_{a}^{b} f(kx) dx$$ But it does not seem right when I actually calculate, I can't understand why... And if it is wrong is there any way to compress it? And is there any name/topic for this type of compressing integrals? I would like to read about it! Thank you in advance!
-
2You are referring to substitution in integrals. You want to do the substitution $\tilde x = x/k$, this will give you the missing factor of $k$. – DominikS Jan 25 '24 at 11:51
-
Hmm, but why do I have to multiply it by $k$? – hyun Jan 25 '24 at 11:53
-
Heuristically: You need to make up for the "compression", since you stretch/shrink it all by a factor $k$. I recommend any book about Calculus - the substitution will be explained there. – DominikS Jan 25 '24 at 11:54
-
1@DominikS Ohhh, it is because $\int f(kx) dx = \frac{1}{k}F(kx)$ right? And then $\int_{ka}^{kb} f(x) dx = k\int_{a}^{b} f(kx) dx$ – hyun Jan 25 '24 at 11:58
1 Answers
There are a ton of questions on this site about changing the limits of integration when invoking a change of variables / substitution. See, for example, change of variables for definite integrals and Why is it that, when using the u-substitution rule, you apply the the function u to the upper and lower limits? . However, this particular problem has a nice geometric intuition and I can't find it already answered on the site, hence I think that it is worth answering separately, even if it is a kind of abstract duplicate.
Geometry
The basic intuition here comes from a result which is usually taught in precalculus classes in the US:
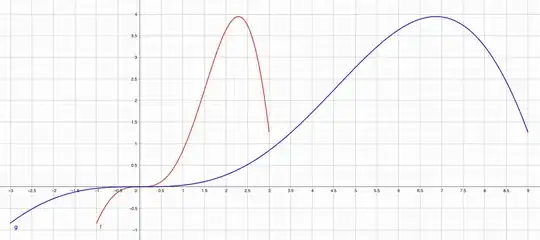
Theorem: Let $f : [a,b] \to \mathbb{R}$ be a function and let $C > 0$. Define a new function $$ g : [Ca, Cb] \to \mathbb{R} : x \mapsto f\left( \frac{1}{C} x \right). $$ The graph of $g$ is identical to the graph of $f$ after a horizontal scaling by a factor of $C$.[1]
I am not going to prove this here, but it is something which is relatively easy to see and build some intuition for using a tool like GeoGebra. For example, in the following image, the function $f$ (in blue) is defined on the interval $[-1,3]$, while the function $g$ (in red) is a scaled copy of $f$, defined by the formula $g(x) = f(x/3)$.
If the integral is interpreted as the area under the curve, then this model makes it more clear that the area under $g$ is exactly $C$ times the area under $f$—horizontally scaling the graph of $f$ by a factor of $C$ scales the area by that same factor. This implies that $$\int_{a}^{b} f(x)\,\mathrm{d}x = C \int_{Ca}^{Cb} f\left( \frac{1}{C} x\right) \,\mathrm{d}x. $$
Change of Variables
Note that this is the result which would be obtained via a more traditional change of variables or substitution: to evaluate $$\int_{ka}^{kb} f(x)\,\mathrm{d}x, $$ define $u = \frac{1}{k} x$. Then $\mathrm{d}u = \frac{1}{k}\,\mathrm{d}x$, and $$ x = ka \implies u = a \qquad\text{and}\qquad x = kb \implies u = b. $$ Therefore $$ \int_{ka}^{kb} f(x)\,\mathrm{d}x = \int_{a}^{b} f(ku) \cdot k\,\mathrm{d}u = k \int_{a}^{b} f(u) \,\mathrm{d}u. $$ This is exactly the same result as above, modulo renaming some of the variables and functions.
Notes
[1] The result actually holds for a function defined on any domain $D \subseteq \mathbb{R}$, and there are more general versions in higher dimensions, but I am choosing to state the theorem for intervals because the goal is to get to a definite integral. Definite (Riemann) integrals are defined for functions on closed intervals, so the version of the theorem stated here is sufficient for the application here.
- 29,772