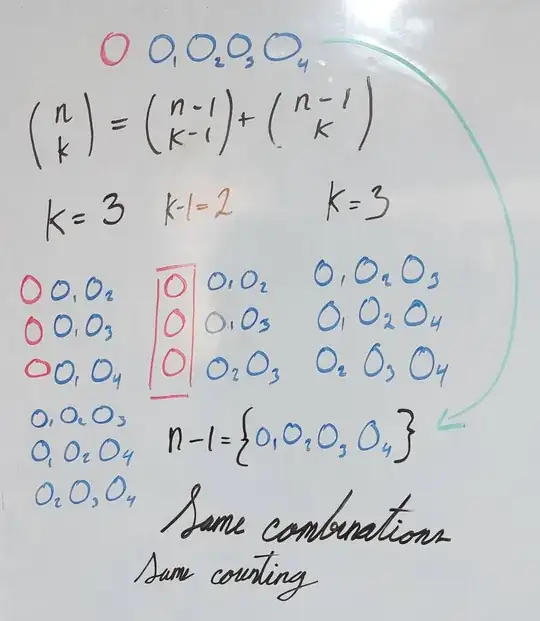I'm trying to understand the combinatorial identity $ \binom{n+1}{k} = \binom{n}{k-1} + \binom{n}{k}. $ I have a good understanding of the algebraic manipulation involved, but I'm struggling with the following interpretation:
Suppose $k$-subset $A = \{0,1,2,3,...,n\}$ where $A$ has $n+1$ elements.
(1) Now, the subset $\binom{n}{k-1}$ can contain the subset of $A$ containing $0$ because to make that a subset, we can start with $\{0\}$ and append an additional $k-1$ numbers selected from $\{1,2,3,...,n\}$, and there are $\binom{n}{k-1}$ ways to do that.
(2) On the other hand, $\binom{n}{k}$ does not contain $0$ since it is the number of ways to select $k$-element subsets from $\{1,2,...,n\}$.
With statement (2), I don't have any issues; I understand that $A = \{0,1,2,...,n\}$ has $n+1$ elements, and if we remove $0$, we are left with the set $\{1,2,...,n\}$ which has $n$ elements. My problem is with statement (1) as I don't understand if we are saying that $A = \{0,1,2,...,n\}$ of length $n+1$ then why it is still there in $\binom{n}{k-1}$? it's because we remove another element to become $\{0,1,2,3,...,n-1\}$? Additionally, I'm not sure what "we can start with $\{0\}$ and append an additional $k-1$ numbers" means. Does it imply that subsets like $\{0,1\}, \{0,2\}$, etc., can be formed?
Any clarification on this would be greatly appreciated.
P.S. I'm concious that this problem is already here in Mathematics StackExchange, but this way of prooving the problem (with the $0$ cases) is not yet. Prove that $\binom{n+1}k = \binom nk + \binom n {k-1}$