Here is a solution, written not to be a quick solution, but rather written
- to show "all" that was found in the given geometric situation, and
- showing more
- and giving all detainls on how it was found based on constructive geometrical means, unfortunately highly supported by the computer.
Algebraically we proceed by also using barycentric / areal coordinates.
Some words on the ad-hoc notations used. Often in situations like the one encountered,
there appear many polynomials in $a^2,b^2,c^2$.
My convention is to use $A,B,C$ algebraically instead, there will be a small chance of confusion with the points $A,B,C$ of the triangle we start with,
but i hope the typed formulas look more compact, so i hesitated, but finally i used this own convention.
We are working in a projective geometry setting.
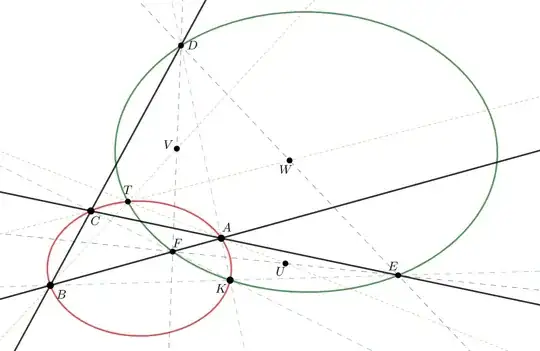
Let's say the conic $ABCKT$ is an ellipse.
Changing the spacial point of view for this conic section, we may and do assume without restricting the general setting that this is a circle.
In fact, every ellipse is an affine image of a circle. The affine transformation can be taken to be a contraction w.r.t. a line, we contract distances
in the direction of the smaller axis, and keep distances for the direction of the bigger axis. So the idea below is the following one.
Start with the general situation from the problem, call it original. Then $ABCKT$ is/determines an ellipse.
Consider the affine transformation $\alpha$ that brings it into a circle. All points $A,B,C,K,T,\dots$ are now points
$\alpha A,\alpha B,\alpha C,\alpha K,\alpha T,\dots$ and we refresh our notations, use a while by abuse
$A,B,C,K,T,\dots$ instead, to make the difference when needed, call this situation the $\alpha$-world. Then the original ellipse $DEFKT$ is transformed in a curve
in the $\alpha$-world, which is also an ellipse. Analytic argument for this may be as follows, chose axes so that the affine contraction is $(x,y)\to(X,Y)=(x,ky)$,
take the original ellipse with an equation of the shape $Mx^2+Nxy+\dots =0$ and rewrite $x,y$ in terms of $X,Y$ to get also a conic. It is clear that a bounded conic
remains bounded after transformation. So $DEFKT$ is in the $\alpha$-world also an ellipse.
(Before and after $\alpha$ we have the same the same incidence, collinearity, projectivity, conic properties. This is important, since we make the same constructions
in the $\alpha$ world, and come back by $\alpha^{-1}$ also conserving them.)
We expect then by the claimed similarity to also have a circle.
And this is the case, as it will be shown below.
What about the case of a hyperbola $ABCKT$? We make a choice of coordinates for $A,B,C,K,T$ in $\Bbb R^2$ so that its equation is
of the shape $x^2/a^2-y^2/b^2=1$. All further constructions are / were done using algebraic geometry with equations of degree $1$ to determine
$D,E,F$. Write the equation of $DEFKT$ now in $(x,y)$-coordinates. It is an equation of the shape
$Mx^2+Nxy+Py^2+\dots=0$, where $M,N,P,\dots$ (seen as projective six-tuple in $\Bbb P^5(\Bbb R)$) vary analytically as "universal" functions of $a,b$.
But in this case we are allowed to extend the domain for $a,b$ from $\Bbb R$ to $\Bbb C$, possibly introducing some singular cases,
and we can recover these functions always if we let $(a,b)$ still take independently infinitely many values.
This allows us to switch from $b\in \Bbb R$ to $b\in i\Bbb R$, so we have an ellipse, and move to the other case.
Let us solve the problem under the ellipse assumption for $ABCKT$.
Lemma A: Let $\Delta ABC$ be a triangle with circumcenter $O=X(3)_{ABC}$ and circumcircle $(O)=(ABC)$.
Consider $K$ a further point on the circumcircle. Let $\Delta DEF$ be the cevian triangle associated with $K$, $D\in BC$, $E\in CA$, $F\in AB$.
Let $\Xi=X(2)_{DEF}$ be the centroid of $\Delta DEF$, and $\Delta UVW$ be its cevian triangle in $\Delta DEF$, so $U,V,W$ are the mid points of $EF,FD,DE$.
Let $\Psi$ be the mid point of the segment $FT$.
Then:
$(i)$ $AU$, $BV$, $CW$ are concurrent in a point $T$.
Assume from now on that $T$ is also a point on the circumcircle $(O)=(ABC)$.
Then: $(ii)$ The points $DEFTK$ are also on a circle $(O')$ with center $O'$.
$(iii)$ The points $OT\Xi K$ are on a circle, centered in a point denoted by $\Upsilon$, the mid point of the diameter $O\Xi$.
$(iv)$ The circumcenter $O$ of $(ABCKT)$, the mid point $\Psi$ of $FK$, the centroid $\Xi$ of $\Delta DEF$, the circumcenter $O'$ of $(DEFTK)$,
and the circumcenter $\Upsilon$ of $OT\Xi K$ are colinear. Let $\color{orange}{(L)}$ be this line.
$(v)$ $L$ is perpendicular on $FK$ (in $\Psi$).

Proof:
We use barycentric coordinates $(x,y,z)$ w.r.t. $\Delta ABC$, with sides of lenghts $a,b,c$. The notation $(x,y,z)$ implicitly assumes the norming condition $x+y+z=1$. If we relax it to $x+y+z\ne 0$, then we write $[x:y:z]$.
Then the involved points, line and circles have the following equations:
$$
\begin{aligned}
A &=(1,0,0)\ ,\\
B &=(0,1,0)\ ,\\
C &=(0,0,1)\ ,\\[2mm]
(O)\qquad 0 &=a^2yz + b^2 zx+c^2xy\ ,\\[2mm]
&\qquad\text{ Convention / abuse of notation: }A=a^2\ ,\ B =b^2\ ,\ C = c^2\ .\\
&\qquad\text{ The the above equation can be rewritten:}\\[2mm]
(O)\qquad 0 &=Ayz + Bzx + Cxy\ ,\\[2mm]
O&=[A(B+C-A)\ :\ B(C+A-B)\ :\ C(A+B-C)]\ ,\\[2mm]
K &= [l:m:n]\ ,\\
D &= [0:m:n]\ ,\\
E &= [l:0:n]\ ,\\
F &= [l:m:0]\ ,\\[2mm]
U &=\frac 12(E+F)\\
&=\frac 12\left(\left(\frac l{l+n},0,\frac n{l+n}\right)
+ \left(\frac l{l+m},\frac m{l+m},0\right)\right)\\
&=\frac 12\left(\frac l{l+n} + \frac l{l+m},\frac m{l+m},\frac n{l+n}\right)
\\
&=[*:m(l+n):n(l+m)]\ ,\\
V &=[l(m+n):*:n(l+m)]\ ,\\
W &=[l(m+n):m(l+n):*]\ ,\\[2mm]
T &=[l(m+n):m(l+n):n(l+m)]\qquad\text{ is on $AU$ because the $(AUT)$ determinant is}\\[2mm]
&\qquad
\begin{vmatrix}
1&0&0\\ *&m(l+n)&n(l+m)\\ *&m(l+n)&n(l+m)
\end{vmatrix}=0\ . \qquad\text{ So $T=AU\cap BV\cap CW$, showing $(i)$ .}
\\[2mm]
(O')\qquad 0 &= -a^2yz-b^2zx-c^2xy+(x+y+z)(ux+vy+wz)\ ,\qquad\text{ where }\\[2mm]
&\qquad 2u = -a^2\frac{mn}{l(m+n)} + b^2 \frac n{l+n}+ c^2 \frac m{l+m}\ ,\\
&\qquad 2v = +a^2\frac n{m+n} - b^2 \frac {ln}{m(l+n)}+ c^2 \frac l{l+m}\ ,\\
&\qquad 2w = +a^2\frac m{m+n} + b^2 \frac l{l+n}- c^2 \frac {lm}{n(l+m)}\ ,\\[2mm]
\Xi &=\frac 13(D+E+F)\\
&=[l(2l+m+n)(m+n)\ :\ m(2m+l+n)(l+n)\ :\ n(2n+l+m)(l+m)]\\
&=[l(e_1+l)(e_1-l)\ :\ m(e_1+m)(e_1-m)\ :\ n(e_1+n)(e_1-n)]\ ,\\
T
&=[l(m+n)\ :\ m(l+n)\ :\ n(l+m)]\\
&=[l(e_1-l)\ :\ m(e_1-m)\ :\ n(e_1-n)]
\ .
\end{aligned}
$$
Above, we have introduced $e_1$, the sum of the variables $l,m,n$,
$e_1=e_1(l,m,n)=l+m+n$, and at this point let us define also
$e_2=e_2(l,m,n)=lm+mn+ln$,
$e_3=e_3(l,m,n)=lmn$, so we have from now on notations for the elementary symmetric polynomials in $l,m,n$.
So far, there is no assumption on $K,T$.
Let us now assume that these points are on $(O)$. So we have
zero in $Ayz+Bzx+Cxy=a^2yz + b^2 zx+c^2xy$ when we plug in the coordinates of $K,T$. So:
$$
\begin{aligned}
0&=\sum A\; mn\ ,\qquad\text{ from $K\in(O)$, and for $T$ now:}\\
0&=
\sum A\; mn(l+m)(l+n)=
\sum A\; mn(l^2+(lm+ln+mn))=
\sum A\; mn\;l^2
\\
&=lmn\sum A\; l\ .
\end{aligned}
$$
We obtain thus the following zero cyclic sums. (We cycle in the same time
$a,b,c$ and $l,m,n$.) It is useful to use $l',m',n'$ for $1/l$, $1/m$, $1/n$
to avoid fractions.
$$
\tag{$*$}
\bbox[yellow]{
\qquad
0=\sum A\;l=\sum A\;mn=\sum \frac Al=\sum Al'\ .
\qquad
}
$$
It may be useful to note that there are two solutions $[l:m:n]$ for the above equations.
Up to a constant we have
$$
l =
A^2B + A^2C + B^2C + BC^2 - B^3 - C^3 - 2ABC
\\
\qquad\qquad
\pm (B-C)\sqrt{-(A+B+C)(B+C-A)(C+A-B)(A+B-C)}
$$
and for $m,n$ use the same sign and cyclic permutations of $A,B,C$.
These solutions are real (true ellipse case),
iff (exactly) one of the quantities $(B+C-A)$, $(C+A-B)$, $(A+B-C)$
is negative, i.e. iff $\Delta ABC$ has an obtuse angle.
The above formula also shows the algebraic complexity of the given situation,
and why there are so many contorsions when trying to show the one or the other equality.
We show now that $K$ is on $(DEF)$ by checking the equation for $K=[l:m:n]$.
This is a first part of $(ii)$.
The sign $\sim$ means equality up to a non-zero factor.
$$
\begin{aligned}
&\underbrace{-a^2\;mn-b^2\;ln-c^2\;lm}_{=0\text{ from }K\in(O)} +(l+m+n)(ul+vm+wn)
\\
&\qquad \sim (l+m+n)(ul+vm+wn)
\\
&\qquad \sim 2(ul+vm+wn)
\\
&\qquad = \left(-A\frac {mn}{m+n} + B\frac {ln}{l+n} + C\frac {lm}{l+m} \right)
\\
&\qquad\qquad + \left(+A\frac {mn}{m+n} - B\frac {ln}{l+n} + C\frac {lm}{l+m} \right)
\\
&\qquad\qquad\qquad + \left(+A\frac {mn}{m+n} + B\frac {ln}{l+n} - C\frac {lm}{l+m} \right)
\\
&\qquad = \left(A\frac {mn}{m+n} + B\frac {ln}{l+n} + C\frac {lm}{l+m} \right)
\\
&\qquad \sim A\;mn(l+m)(l+n) + B\;ln(m+l)(m+n) + C\;lm(n+l)(n+m)
\\
&\qquad=0\ ,\qquad\text{ from the assumption $T\in(O)$, relation $(*)$ above .}
\end{aligned}
$$
We show that $T$ is on $(DEF)$ by checking the equation for $T=[l(m+n):m(l+n):n(l+m)]=[x_T:y_t:z_T]$.
This is the second part of $(ii)$.
The sign $\sim$ means equality up to a non-zero factor.
$$
\begin{aligned}
&\underbrace{-a^2\;y_Tz_T-b^2\; z_Tx_T-c^2\;x_Ty_T}_{=0\text{ from }K\in(O)}
+(\dots)(ux_T+vy_T+wz_T)
\\
&\qquad \sim 2(ux_T+vy_T+wz_T)
\\
&\qquad \sim 2(u\;l(m+n)+v\;m(l+n)+w\;n(l+m))
\\
&\qquad = \left(-A\;mn + B\frac {ln}{l+n}(m+n) + C\frac {lm}{l+m}(m+n) \right)
\\
&\qquad\qquad +
\left(+A\frac {mn}{m+n}(l+n) - B\; ln + C\frac {lm}{l+m}(l+n) \right)
\\
&\qquad\qquad\qquad + \left(+A\frac {mn}{m+n}(l+m) + B\frac {ln}{l+n}(l+m)
- C\; lm \right)
\\
&\qquad = 2lmn\left(A\frac 1{m+n} + B\frac 1{l+n} + C\frac 1{l+m} \right)
\\
&\qquad \sim A\;(l+m)(l+n) + B\;(m+l)(m+n) + C\;(n+l)(n+m)
\\
&\qquad =\sum A\;(l^2+lm+ln+mn)
\\
&\qquad =\sum A\;(l^2+lm+ln)+\underbrace{\sum A mn}_{=0}
\\
&\qquad =(l+m+n)\sum Al
\\
&\qquad=0\ .
\end{aligned}
$$
This shows that the conic $DEFKT$ is also a circle - centered in $O'$.
(However, the coordinates of $O'$ are not yet computed/isolated.)
We have shown $(ii)$.
So far we know that if $ABCKT$ is a circle, then $DEKFT$ is also a circle.
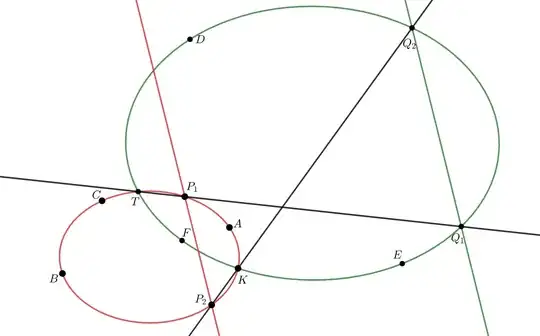
They have then two centers of homothety, in the picture denoted by $S,S'$, for $S$ we have a positive factor, for $S'$ a negative factor.
The points were constructed by drawing the diameters perpendicular on $OO'$.
For the solution in the general case we need a strategy to put the hands on $O';S,S'$, or at least on the axis $OO'SS'$.
The further points of Lemma A go in this direction.
We cover $(iii)$ now.
From $(ii)$ we know that $OK=OT$ (from $K,T\in (O)$), and that $O'K=O'T$ (from $K,T\in (O')$).
Let us show that $\Xi$ also shares this property of the perpendicular bisector of the segment $KT$.
We show first that the point $\Psi$, mid point of $KT$, is on $O\Xi$.
This will be a long computation from the point of view of a human, i tried to do it explicitly.
Postponed is the computer version, which is deceptively short, we ask if a relation is an ideal, and get a laconic True
as answer. The human computation now.
The point $\Psi$ is
$$
\begin{aligned}
\Psi
&=
\frac 12(K+T)
\\
&=\frac12\left(\left(\frac l{l+m+n}\ ,\ \dots\ ,\ \dots\right)
+\left(\frac{l(m+n)}{2(mn+lm+ln)}\ ,\ \dots\ ,\ \dots\right)\right)
\\
&=\frac14\left(\frac {2l(mn+lm+ln)+l(m+n)(l+m+n)}{(l+m+n)(mn+lm+ln)},\dots\right)
\\
&=[2l(mn+lm+ln)+l(m+n)(l+m+n)\ :\ \dots\ :\ \dots]
\\
&=[2le_2 + le_1(e_1-l)\ :\ 2me_2+me_1(e_1-m)\ :\ 2ne_2+ne_1(e1-n)]\ .
\end{aligned}
$$
So the components of $\Psi$ involve only $l,m,n$.
The same is also the case for the components of $\Xi$.
We consider the determinant with lines extracted from the coordinates of $O,\Psi,\Xi$,
and expand w.r.t. the first line hoping to be able to use the relation $(*)$.
Denoting by $x_\Psi,y_\Psi, z_\Psi$ coordinates for $\Psi$, and $x_\Xi,y_\Xi,z_\Xi$ those for $\Xi$,
we thus want to compute the following determinant $\Delta_{O,\Psi,\Xi}$ and show it is vanishing:
$$
\begin{aligned}
\Delta_{O,\Psi,\Xi}
&=
\begin{vmatrix}
A(B+C-A) & B(C+A-B) & C(A+B-C)\\
x_\Psi & y_\Psi & z_\Psi\\
x_\Xi & y_\Xi &z_\Xi
\end{vmatrix}
\\
&=
\sum
A(B+C-A)
\begin{vmatrix}
y_\Psi & z_\Psi\\
y_\Xi &z_\Xi
\end{vmatrix}\ ,\text{ so let us consider}
\\
\begin{vmatrix}
y_\Psi & z_\Psi\\
y_\Xi &z_\Xi
\end{vmatrix}
&=
\begin{vmatrix}
2me_2 + me_1(e_1-m) & 2ne_2 + ne_1(e_1-n)\\
m(e_1+m)(e_1-m) & n(e_1+n)(e_1-n)
\end{vmatrix}
\text{ (use now linearity w.r.t. first row)}
\\
&=2mn e_2
\begin{vmatrix}
1 & 1\\ e_1^2 - m^2 & e_1^2 - n^2
\end{vmatrix}
+
mn e_1(e_1-m)(e_1-n)
\begin{vmatrix}
1 & 1\\ e_1 + m & e_1 + n
\end{vmatrix}
\\
&=2mn e_2(m^2-n^2) - mne_1(e_1-m)(e_1-n)(m-n)
\\
&=2mn e_2(e_1-l)(m-n) - mne_1(e_2-l^2)(m-n)
\\
&=(m-n)( mn e_1e_2 - 2e_2e_3 - e_1e_3 l)
\\
&=(m-n)e_3( l'e_1e_2 - 2e_2 - e_1 l)
\\
&\qquad\text{ where, recall, $l',m',n'$ are $1/l$, $1/m$, $1/n$ ,}
\\[3mm]
\Delta_{O,\Psi,\Xi}
&=
\sum
A(B+C-A)
\begin{vmatrix}
y_\Psi & z_\Psi\\
y_\Xi &z_\Xi
\end{vmatrix}
\\
&=
e_1e_2e_3
\begin{vmatrix}
Al'(B+C-A) & Bm'(C+A-B) & Cn'(A+B-C)\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
\\
&\qquad
-
2e_2e_3
\begin{vmatrix}
A(B+C-A) & B(C+A-B) & C(A+B-C)\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
\\
&\qquad\qquad-
e_1e_3
\begin{vmatrix}
Al(B+C-A) & Bm(C+A-B) & Cn(A+B-C)\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
\ .
\\[3mm]
&\qquad\text{ Let $\Delta_1,\Delta_2,\Delta_3$ be the above determinants.}
\\[3mm]
&\qquad\text{ We must show $e_1e_2\Delta_1-2e_2\Delta_2-e_1\Delta_3=0$.}
\\[3mm]
&\qquad\text{ We will show $e_1\Delta_1=3\Delta_2$ and $e_2\Delta_2= e_1\Delta_3$.}
\\[3mm]
&\qquad\text{ First, let us consider $e_2\Delta_2= e_1\Delta_3$.}
\\[3mm]
e_2\Delta_2-e_1\Delta_3
&=
\begin{vmatrix}
Ae_2(B+C-A) & \dots &\dots \\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
-
\begin{vmatrix}
Ale_1(B+C-A) & \dots & \dots\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
\\
&=
\begin{vmatrix}
A(mn-l^2)(B+C-A) & \dots &\dots \\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
=
\begin{vmatrix}
Amn(B+C-A) & \dots & \dots\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
-
\begin{vmatrix}
Al^2(B+C-A) & \dots & \dots\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
\\
&=
e_3
\begin{vmatrix}
Al'(B+C-A) & \dots & \dots\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
-
e_3
\begin{vmatrix}
Al(B+C-A) & \dots & \dots\\
l' & m' & n'\\
1 & 1 & 1
\end{vmatrix}
\\
&=
e_3
\begin{vmatrix}
Al'(B+C-A) & \dots & \dots\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
+e_3
\begin{vmatrix}
Al(B+C-A) & \dots & \dots\\
1 & 1 & 1 \\
l' & m' & n'
\end{vmatrix}
\\
&=e_3(\Delta_1+\Delta'_1)
\\
&\sim(\Delta_1+\Delta'_1)
\ ,
\\
&\qquad\text{ and we have a "prime"-symmetric expression w.r.t. $l,m,n\leftrightarrow l',m',n'$.}
\\
&\qquad\text{ We compute $\Delta_1$, the "prime"-version $\Delta'_1$ is get by symmetry.}
\\
&\qquad\text{ Note the relation:}
\\
&\qquad\qquad Bm'(A+C-B)-Al'(B+C-A)
\\
&\qquad\qquad\qquad = Bm'(A+C-B)+(Bm'+Cn')(B+C-A)
\\
&\qquad\qquad\qquad = 2BCm' +Cn'(B+C-A)\ ,
\\
\Delta_1 &=\begin{vmatrix}
Al'(B+C-A) & \dots & \dots\\
1 & 1 & 1\\
l & m & n
\end{vmatrix}
&=
\begin{vmatrix}
* & 2BCm' +Cn'(B+C-A) & 2BCn' +Bm'(B+C-A)\\
1 & 0 & 0\\
* & m-l & n-l
\end{vmatrix}
\\
&\sim
\begin{vmatrix}
2BCm' +Cn'(B+C-A) & 2BCn' +Bm'(B+C-A)\\
m-l & n-l
\end{vmatrix}
\\
&=
2BC
\begin{vmatrix}
m' & n' \\
m-l & n-l
\end{vmatrix}
+
(B+C-A)
\begin{vmatrix}
Cn' & Bm'\\
m-l & n-l
\end{vmatrix}
\ ,\qquad\text{ so}\\[3mm]
e_2\Delta_2-e_1\Delta_3
&\sim \Delta_1+\Delta_1'
\\
&=
2BC
\begin{vmatrix}
m' & n' \\
m-l & n-l
\end{vmatrix}
+
2BC
\begin{vmatrix}
m & n \\
m'-l' & n'-l'
\end{vmatrix}
\\
&\qquad
+
(B+C-A)
\begin{vmatrix}
Cn' & Bm'\\
m-l & n-l
\end{vmatrix}
+
(B+C-A)
\begin{vmatrix}
Cn & Bm\\
m'-l' & n'-l'
\end{vmatrix}
\\
&=
-2BC(l(m'-n')+l'(m-n))
+(B+C-A)
\begin{vmatrix}
C & B\\
2-m'l-ml' & 2-n'l-nl'
\end{vmatrix}
\\
&=C(n'l+nl')(B+A-C)-B(m'l+ml')(A+C-B)+2(C^2-B^2+AB-AC)
\\
&=-(Al'l+Bm'l+All'+Bml')(B+A-C)
\\
&\qquad -B(m'l+ml')(A+C-B)+2(C^2-B^2+AB-AC)
\\
&=-2A(B+A-C)-2AB(m'l+ml')+2(C^2-B^2+AB-AC)
\\
&\sim -A^2-AB(m'l+ml') +C^2-B^2
\\
&= -A^2 - (Bm')(Al) - (Al')(Bm) +C^2-B^2
\\
&= -A^2 + (Al'+Cn')(Al)+ (Bm'+Cn')(Bm) +C^2-B^2
\\
&= (Cn')(Al)+ (Cn')(Bm) + (Cn')(Cn)
\\
&=0\ .
\end{aligned}
$$
At this point we have humanly only the half of the work for $(iii)$,
and since the space is limited, i have to switch to the computer aided proof.
Which is deceptively simple as said.
We will work in the ring $R=\Bbb Q[A,B,C;l,m,n]$, localized in $l,m,n$, with the ideal generated by the relation
$l+m+n=1$ and the relations $(*)$, which are $0=\sum Al=\sum Al'$. Then we simply ask if a relation
is satisfied in $J$. We use l1, m1, n1 for the inverses of l, m, n.
R.<A,B,C,l,m,n,l1,m1,n1> = QQ[]
e1 = l + m + n
e2 = lm + mn + nl
e3 = lm*n
J = R.ideal([
l + m + n - 1,
ll1 - 1, mm1 - 1, nn1 - 1,
Al + Bm + Cn,
Al1 + Bm1 + C*n1])
O = vector([A(B + C - A), B(C + A - B), C*(A + B - C)])
Psi = vector([2le2 + l(m + n)e1, 2me2 + m(l + n)e1, 2ne2 + n(l + m)e1])
Xi = vector([l(e1 + l)(e1 - l), m(e1 + m)(e1 - m), n(e1 + n)(e1 - n)])
Are the points O, Psi, Xi with the above (inhomogeneous) coordinates COLLINEAR?
We check for the vanishing of the determinant built by them.
print(f"Are O, Psi, Xi collinear? {matrix(3, 3, [O, Psi, Xi]).det() in J}")
And we obtain:
Are O, Psi, Xi collinear? True
It may be useful to also check the relation claimed above.
We define $\Delta_1,\Delta_2,\Delta_3$ as the determinants of the matrices
M1, M2, M3, and check the claimed relations.
M1 = matrix(3, 3, [A*l1*(B + C - A), B*m1*(C + A - B), C*n1*(A + B - C),
1, 1, 1,
l, m, n])
M2 = matrix(3, 3, [A(B + C - A), B(C + A - B), C*(A + B - C),
1, 1, 1,
l, m, n])
M3 = matrix(3, 3, [Al(B + C - A), Bm(C + A - B), Cn(A + B - C),
1, 1, 1,
l, m, n])
And now, in dialog with sage:
sage: e1*e2*M1.det() - 2*e2*M2.det() - e1*M3.det() in J
True
sage: e1*M1.det() - 3*M2.det() in J
True
sage: e2*M2.det() - e1*M3.det() in J
True
A further check for $\Delta_1+\Delta_1'=0$:
M1prime = matrix(3, 3, [A*l*(B + C - A), B*m*(C + A - B), C*n*(A + B - C),
1, 1, 1,
l1, m1, n1])
And now:
sage: M1.det() + M1prime.det() in J
True
So far we know that $OT=OK$, so the perpendicular bisector of $TK$ is the line $O\Psi$,
$\Psi$ being the mid point of $TK$, and $\Xi$ is a point of this line.
The details so far insure $(iv)$ and $(v)$.
In order to finish $(iii)$ we have to show $OT\perp T\Xi$ and/or
$OK\perp K\Xi$.
Computer check to finish in time.
We build the displacement vectors $\overrightarrow{OK}:=K-O$ and $\overrightarrow{K\Xi}=\Xi - K$
using normed coordinates for the involved points,
denote by
$(x_1,y_1,z_1)$ and
$(x_2,y_2,z_2)$ their coordinates (that sum to zero),
and check the relation:
$$
\sum A(y_1z_2+y_2z_1) =0\ .
$$
R.<A,B,C,l,m,n,l1,m1,n1,E2> = QQ[]
e1 = l + m + n
e2 = l*m + m*n + n*l
e3 = l*m*n
J = R.ideal([
l + m + n - 1,
ll1 - 1, mm1 - 1, nn1 - 1, e2E2 - 1,
Al + Bm + Cn,
Al1 + Bm1 + Cn1])
O = vector([A(B + C - A), B(C + A - B), C*(A + B - C)])
Xi = vector([l(e1 + l)(e1 - l), m(e1 + m)(e1 - m), n(e1 + n)(e1 - n)])
K = vector([l, m, n])
O, Xi, K = O/sum(O), Xi/sum(Xi), K/sum(K) # norming
x1, y1, z1 = K - O
x2, y2, z2 = Xi - K
rel = ( A(y1z2 + y2z1) + B(z1x2 + z2x1) + C(x1y2 + x2*y1) ).numerator()
print(f"Is rel in J? {rel in J}")
And we obtain:
Is rel in J? True
So finally we also have $OK\perp K\Xi$.
This concludes $(iii)$ and the Lemma A.
To avoid complicated computations, let us give a plain exact example with explicit numbers.
In the following picture we have $A,B,C=64,9,77$.
The triangle $\Delta ABC$ has thus the sides $a,b,c=8,3,\sqrt {77}$.

The values were chosen to have a small amount of square roots below, and are "random enough"
to reveal optically only general geometric properties.
The chosen point $K$ that makes the corresponding $T$ land also on $(O)$
is $K=\frac1{53}(21 A+56B -24C)$. There is exactly one other point, that may have worked,
$K'=\frac 14(8A+3B-7C)$ that may have also worked, but $K$ makes the picture more together.
The given triangle has area $S$ given by $S^2=s(s-a)(s-b)(s-c)=\frac1{16}(2AB+2BC+2CA-A^2-B^2-C^2)
=\frac 1{16}(1152+1386+9856-4096-81-5929)=\frac 1{16}(2288)=143$. So $S=\sqrt {143}$.
We compute the radius $R=abc/(4S)=\frac{6\sqrt{77}}{\sqrt{143}}$.
Similarly we can proceed for the triangle $\Delta DEF$.
The sides are
$EF=\sqrt{5376/11}$,
$DF=\sqrt{756/11}$,
$DE=14\sqrt 3$.
The corresponding area is
$[DEF]=\sqrt{91728/11}$. And its circumradius is
$R'=\frac{84\sqrt 3}{\sqrt{143}}$.
So we have the ratio of homothety $R/R'=\frac{\sqrt{11}}{2\sqrt{21}}$.
At last now, it is time to see that $\Delta ABC$ and $\Delta DEF$ are similar.
(In geogebra one can show the angles, and there is a coincidence of values up to all shown decimal places.)
This leads to the following Lemma.
Lemma B:
The triangles $\Delta ABC$ and $\Delta DEF$ are similar under the condition $(*)$.
Proof:
It is enough to show
$$
\frac {EF^2}A=\frac{DF^2}B=\frac{DE^2}C\ .
$$
By symmetry, it is enought to show the first equality. The displacement vector from $E$ to $F$ is
$$
F-E
=\left(\frac {l(n-m)}{(l+m)(l+n)}\ ,\ \frac m{l+m}\ ,\ -\frac n{l+n}\right)\ .
$$
Let $x,y,z$ be the above components. Then $EF^2$ is $-A^2yz-B^2zx-C^2xy$.
Its common denominator is $(l+m)^2(l+n)^2$, and the numerator is after forcing the factor $e_3=lmn$ easy to reshape:
$$
\begin{aligned}
&(l+m)^2(l+n)^2\;EF^2
\\
&=e_3\Big(\ (Al+Am+An+Amnl')
\\
&\qquad + (-Bl-Bm+Blnm'+Bn) +(-Cl+Cm+Clmn'-Cn)\ \Big)
\\
&=e_3\Big(\ (Al+Am+An-mn(Bm'+Cn'))
\\
&\qquad + (-Bl-Bm-Bln(Al'+Cn')+Bn) +(-Cl+Cm+lm(Al'+Bm')-Cn)\ \Big)
\\
&=-2le_3(B+C-A)\ .
\end{aligned}
$$
So for $EF^2:A=DF^2:B$ it is enough to show the equality
$$
\frac{2l(B+C-A)}{A(l+n)^2} =
\frac{2m(A+C-B)}{B(m+n)^2} \ .
$$
We compute for this:
$$
\begin{aligned}
&Bm'(B+C-A)(m+n)^2 - Al'(A+C-B)(l+n)^2
\\
&\qquad=B(B+C-A)(m+2n) -A(A+C-B)(l+2n)\\
&\qquad\qquad+Bm'(B+C-A)n^2 -Al'(A+C-B)n^2
\\
&\qquad=Bm(B+C-A)-Al(A+C-B)\\
&\qquad\qquad+2n(B^2+BC-A^2-AC)\\
&\qquad\qquad\qquad + n^2(BCm' -ACl')
+n^2(B^2m'+ABl' -ABm'-A^2l')
\\
&\qquad=Bm(B+C-A)+(Bm+Cn)(A+C-B)\\
&\qquad\qquad+2Cn(B-A) +2nB^2 -2n(Al)(Al')\\
&\qquad\qquad\qquad + n^2(2BCm' + C^2n')
+n^2(B(-Cn') -A(-Cn'))
\\
&\qquad=0\ .
\end{aligned}
$$
$\square$
Lemma C:
The points $UVWTK$ are on a circle. Let $\Lambda$ be its center.
Then since $\Delta DEF$ and $\Delta UVW$ are similar w.r.t. the perspector $\Xi$ and factor $UV:DE=1:2$
we have $\Lambda,\Xi,O'$ collinear and $\Lambda\Xi:\Xi O'=1:2$.
Moreover, $O,\Upsilon$ complete the chain of rational proportions on the line $(L)=O\Upsilon\Lambda\Xi O'$:
$$
O\Upsilon:\Upsilon\Lambda:\Lambda\Xi:\Xi O'=2:1:1:2\ .
$$

Proof: Skipped.
(The equivalent non-trivial point is about the location of the center $O'$ of the circle $\odot(DEF)$,
that given $O,\Xi$, arguably easier points, we have )
So far, all points that were introduced, excepting $O'$ are on the one or the other circle centered on a point on $(L)$,
and orthogonal to $(L)$.
The properties so far can be in part restated to use a language that also applies to the general case of an ellipse.
This
is an easy translation exercise when the properties are already collected,
and let us do this, since it may be useful when simpler proofs are searched in the ellipse world.
As a matter of notation, for a point $X$ we denote by $x$ (passage to lower case letter) its polar w.r.t. the circle / to the ellipse $ABCKT$.
For a line $x$ we denote by $X$ (capitalized notation) its pole w.r.t. the same circle / ellipse.
For two points $X,Y$ we denote by $XY$ the line which is incident to (i.e. passes through) $X$ and $Y$.
For two lines $x,y$ we denote by $xy$ the points which is incident to (i.e. lies on) $x$ and $y$.
Lemma D: Let $A,B,C;K;D,E,F;U,V,W;T$ be constructed in the original world by the OP-receipt.
Let $\Xi$ be the centroid of $\Delta DEF$ and $\Delta UVW$.
$(i1)$ The polar of $D$ is the line $d=EF$.
$(i2)$ The polar of $E$ is the line $e=DF$.
$(i3)$ The polar of $F$ is the line $f=DE$.
$(j1)$ The pole of $EF$ is the point $ef=e\cap f=DF\cap DE=D$.
$(j2)$ The pole of $DF$ is the point $df=d\cap f=EF\cap DE=E$.
$(j3)$ The pole of $DE$ is the point $de=d\cap e=EF\cap DF=F$.
$(ii)$ The polar of $\Xi$ is the line $\xi=TK$.
$(iii1)$ The polar of $K$ is the line $k=K\Xi$, the tangent in $K$ to the ellipse.
$(iii2)$ The polar of $T$ is the line $t=T\Xi$, the tangent in $T$ to the ellipse.
$(iv1)$ The polar of $U$ is the line $u$ through $D$ and the point $\xi d=TK\cap EF$.
$(iv2)$ The polar of $V$ is the line $v$ through $E$ and the point $\xi e=TK\cap DF$.
$(iv3)$ The polar of $W$ is the line $w$ through $F$ and the point $\xi f=TK\cap DE$.
Proof:
$(i1)$ is a known property, in fact the known construction of the polar of a point.
We have $D= AK\cap BC$ with points $A,B,C,K$ on the ellipse. Then the polar is the line through
$AB\cap CK=F$ and $AC\cap BK=E$.
Properties $(i2)$, $(i3)$ are cyclic versions of $(i1)$.
The properties $(j1)$, $(j2)$, $(j3)$ are dual / reciprocal to $(i1)$, $(i2)$, $(i3)$.
$(ii)$ needs Lemma A, $(iii)$, which insures in the circle case that the inversion $*$ w.r.t. $(O)$ maps $\Psi^*=\Xi$ and $\Xi^*=\Psi$,
so the polar $\xi$ of $\Xi$ is the line perpendicular in $\Psi$ on $O\Xi$, which is $TK$. We need in fact only $OK\perp K\Xi$.
$(iii1)$ uses $(ii)$, the fact that the tangent in $K$ is $K\Xi$. And $(iii2)$ is "the same game" with $K$ replaced by $T$.
For $(iv1)$, note that $U=D\Xi\cap EF$. The line $D\Xi$ has the pole $d\xi=d\cap \xi=EF\cap TK$. The line $EF=d$ has the pole $D$.
So the polar $u$ of $U$ passes through this two points, $EF\cap TK$ and $D$.
Properties $(iv2)$, $(iv3)$ are cyclic versions of $(iv1)$.
$\square$
Conclusion:
We could restrict to the ellipse case by an argument inside the algebraic geometry.
We have furthermore restricted to the case of a circle.
In this case, it turns out that not only the ellipse $DEFKT$ has the same shape, but also
the ellipse $UVWKT$, and the ellipse centered on the line $O\Xi$ through $OTK\Xi$.
Moreover, the point $\Xi$ is on the tangents in $T,K$ to the ellipse $DEFKT$.
The two centers of similitude $S,S'$ of the ellipses $ABCKT$ and $DEFKT$ are on the line $O\Xi$,
with two "easy" points $O,\Xi$, when computations are needed for the one or the other purpose.
However, the concrete location and the factor of similitude are involved.
A simple formula for this factor $\varphi$ is extracted in the circle case from
Lemma B as
$$
\varphi^2
=
\frac{EF^2}A
=
\frac{-2le_3(B+C-A)}{A(l+m)^2(l+n)^2}
$$
And now inserting the special case with $A,B,C=
64,9,77$, and
$l,m,n=\frac 1{53}(21,56,-24)$
in this formula, we get if i have no error on that sheet of paper
$\varphi^2=84/11$ a fairly simple expression.
An expression for $S$ (or $S'$) can be also quickly obtained, since we "know" $R,R'$.
But in the general case a characterization of $S,S'$ is missing so far.
I have to stop here, so i will submit the above. It was a lot of fun for the given geometric configuration,
thanks for the post, i would be nice to have a better echo for this question (and other similar MSE ones).