In this question I use the term "nested Fourier series representation" to refer to an infinite series of one or more Fourier series versus a single Fourier series. Whereas a single Fourier series is periodic, a nested Fourier series representation is not necessarily periodic. When it is periodic it can be expressed as a single Fourier series, and therefore doesn't provide as much increased utility. The nested Fourier series representations for $f(x)$ defined in this question are of the non-periodic nature and even seem to converge globally for $x\in\mathbb{C}$ when $f(x)$ is a complex analytic function for which the Fourier inversion theorem holds.
A long time ago I noticed many series representations of functions derived from Mellin convolutions such as
$$f(s)=\left[\delta(x-1)\,*_\mathcal{M}\,f(x)\right](s)=\int_0^\infty\delta(x-1)\, f\left(\frac{s}{x}\right)\,\frac{dx}{x}\tag{1}$$
seem to converge for $\Re(s)>0$ (and in some cases for $\Re(s)\ge 0$) when formula (1) above is evaluated term-wise using nested Fourier series representations such as
$$\delta(x-1)=\underset{\substack{N, f\to\infty \\ M(N)=0}}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\mu(n)}{n} \left(1+2 \sum\limits_{k=1}^{f n} \cos\left(\frac{2 \pi k x}{n}\right)\right)\right)\tag{2}$$
and
$$\delta(x-1)=\underset{N, f\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\mu(2 n-1)}{2 n-1} \left(\frac{1}{2}+\sum\limits_{k=1}^{2 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k x}{2 n-1}\right)\right)\right)\tag{3}$$
where the evaluation frequency $f$ in the inner sum over $k$ in formulas (2) and (3) above is assumed to be a positive integer.
In Formula (2) above, the upper evaluation limit $N$ in the outer sum over $n$ must be selected such that $M(N)=0$ where
$$M(x)=\sum\limits_{n=1}^x \mu(n)\tag{4}$$
is the Mertens function (which has an infinite number of zeros), whereas formula (3) above eliminates this conditional convergence requirement.
Formulas (2) and (3) above actually converge (in a distributional sense) to $\delta(x+1)+\delta(x-1)$, but the $\delta(x+1)$ term doesn't affect the Mellin convolution defined in formula (1) above since the integral is over $0\le x\le\infty$.
In this answer to one of my own questions on MSE, I posted several examples of formulas derived from Mellin convolutions such as formula (1) above using the analytic representation for $\delta(x-1)$ defined in formula (2) above (see formulas (52) to (70) at my linked answer). As I mentioned above, many of these formulas converge for $\Re(s)>0$ which seems consistent with the fact that many Mellin transforms seem to converge for some subset of $s\in\mathbb{C}$ (e.g. $\Re(s)>\alpha$ for some $\alpha\in\mathbb{R}$).
More recently I noticed many times it seems the function $f(x)$ can be approximated by the nested Fourier series representation
$$f(x)\approx \underset{N, f\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\mu(2 n-1) }{2 n-1} \left(\frac{3 F(0)}{8}\\+\frac{1}{2} \sum\limits_{k=1}^{2 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k}{2 n-1}\right) \left(F\left(\frac{k}{4 n-2}\right) e^{\frac{i \pi k x}{2 n-1}}+F\left(-\frac{k}{4 n-2}\right) e^{-\frac{i \pi k x}{2 n-1}}\right)\\-\frac{1}{8} \sum\limits_{k=1}^{4 f (2 n-1)} (-1)^k\, \left(F\left(\frac{k}{8 n-4}\right) e^{\frac{i \pi k x}{4 n-2}}+F\left(-\frac{k}{8 n-4}\right) e^{-\frac{i \pi k x}{4 n-2}}\right)\right)\right)\tag{5}$$
where
$$F(\omega)=\mathcal{F}_x[f(x)](\omega)=\int\limits_{-\infty}^\infty f(x)\, e^{-2 \pi i \omega x}\, dx\tag{6}$$
is the Fourier transform of $f(x)$ and
$$f(x)=\mathcal{F}_{\omega}^{-1}[F(\omega)](x)=\int\limits_{-\infty}^\infty F(\omega)\, e^{2 \pi i x \omega}\, d\omega\tag{7}$$
is the related inverse Fourier transform.
Formula (5) above is based on the Fourier convolution
$$f(x)=[\delta(y)\,*\,f(y)](x)=\int\limits_{-\infty}^\infty \delta(y)\, f(y-x)\, dy\tag{8}$$
evaluated term-wise using the nested Fourier series representation
$$\delta(x)=\underset{N, f\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\mu(2 n-1)}{2 n-1} \left(\frac{3}{8}+\sum\limits_{k=1}^{2 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k}{2 n-1}\right) \cos\left(\frac{\pi k x}{2 n-1}\right)\\-\frac{1}{4} \sum\limits_{k=1}^{4 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k x}{2 (2 n-1)}\right)\right)\right)\tag{9}$$
which is derived from formula (3) above (see this answer I posted to one of my own questions on MathOverflow).
I believe formula (9) above evaluated at $N=\infty$ is equivalent to the limit representation
$$\delta(x)=\underset{f\to\infty}{\text{lim}}\int\limits_{-f}^f e^{2 i \pi x t} \, dt=\underset{f\to\infty}{\text{lim}}2 f\, \text{sinc}(2 \pi f x)\tag{10}.$$
Formula (5) above is derived from formulas (8) and (9) above using the convolution theorem.
When $f(x)$ is an even function formula (5) above simplifies to
$$f(x)\approx \underset{N, f\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\mu(2 n-1)}{2 n-1} \left(\frac{3 F(0)}{8}\\+\sum _{k=1}^{2 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k}{2 n-1}\right)\, F\left(\frac{k}{4 n-2}\right)\, \cos\left(\frac{\pi k x}{2 n-1}\right)\\-\frac{1}{4} \sum\limits_{k=1}^{4 f (2 n-1)} (-1)^k\, F\left(\frac{k}{8 n-4}\right)\, \cos\left(\frac{\pi k x}{4 n-2}\right)\right)\right),\quad f(-x)=f(x)\tag{11}.$$
When $f(x)$ is an odd function formula (5) above simplifies to
$$f(x)\approx \underset{N, f\to\infty}{\text{lim}}\left(i \sum\limits_{n=1}^N \frac{\mu(2 n-1)}{2 n-1} \\\left(\sum\limits_{k=1}^{2 f (2 n-1)} (-1)^k\, \cos\left(\frac{\pi k}{2 n-1}\right)\, F\left(\frac{k}{4 n-2}\right)\, \sin\left(\frac{\pi k x}{2 n-1}\right)\\-\frac{1}{4} \sum\limits_{k=1}^{4 f (2 n-1)} (-1)^k\, F\left(\frac{k}{8 n-4}\right)\, \sin\left(\frac{\pi k x}{4 n-2}\right)\right)\right),\quad f(-x)=-f(x)\tag{12}.$$
Question: Can the Fourier inversion theorem be stated as follows? If the statement below is too broad, is there a way to qualify it with a set of conditions on $f(x)$ and/or $F(\omega)$ where it holds?
A function $f(x)$ can be recovered from its Fourier transform $F(\omega)$ if-and-only-if the nested Fourier series representation of $f(x)$ converges for $x\in\mathbb{R}$.
The statement above is not intended to preclude convergence over a wider range such as $\Im(x)<\alpha$ when $f(x)$ is a meromorphic function with poles at $x=\pm i \alpha$ for example, or even $x\in\mathbb{C}$ in the case of complex analytic functions. In general I believe when $f(x)$ is recoverable from $F(\omega)$, the nested Fourier series representation for $f(x)$ converges under the same conditions for which the inverse Fourier transform integral defined in formula (7) above converges even though the Fourier transform $F(\omega)=\mathcal{F}_x[f(x)](\omega)$ and inverse Fourier transform $f(x)=\mathcal{F}_{\omega}^{-1}[F(\omega)](x)$ are generally only considered to be valid for $\omega, x\in\mathbb{R}$.
Table (1) below contains a list of example functions whose nested Fourier series representations seem to converge consistent with the conditions described in the previous paragraph. $F(x)$ in row 8 of Table (1) below is the Dawson function.
Table (1): Examples of functions $f(x)$ recoverable from their Fourier transform
$$\begin{array}{cccccc} \# & f(x) & F(\omega ) & \text{Convergence} & \int_{-\infty }^{\infty } | f(x)| \, dx & \int_{-\infty }^{\infty } | F(\omega )| \, d\omega \\ 1 & e^{-x^2} & \sqrt{\pi } e^{-\pi ^2 \omega ^2} & x\in \mathbb{C} & \sqrt{\pi } & 1 \\ 2 & -2 x e^{-x^2} & 2 i \pi ^{3/2} e^{-\pi ^2 \omega ^2} \omega & x\in \mathbb{C} & 2 & \frac{2}{\sqrt{\pi }} \\ 3 & e^{-\frac{x^2}{2}} \left(4 x^2-2\right) & 2 \sqrt{2 \pi } e^{-2 \pi ^2 \omega ^2} \left(1-8 \pi ^2 \omega ^2\right) & x\in \mathbb{C} & 2 \sqrt{2} \left(\sqrt{\pi } \left(1-2 \text{erf}\left(\frac{1}{2}\right)\right)+\frac{4}{\sqrt[4]{e}}\right) & 2-4 \text{erf}\left(\frac{1}{2}\right)+\frac{8}{\sqrt[4]{e} \sqrt{\pi }} \\ 4 & \text{sech}(x) & \pi \text{sech}\left(\pi ^2 \omega \right) & -\frac{\pi }{2}<\Im(x)<\frac{\pi }{2} & \pi & 1 \\ 5 & \frac{1}{x^2+1} & \pi e^{-2 \pi | \omega | } & -1<\Im(x)<1 & \pi & 1 \\ 6 & e^{-| x| } & \frac{2}{4 \pi ^2 \omega ^2+1} & x\in \mathbb{R} & 2 & 1 \\ 7 & 2 \text{sinc}(2 \pi x) & \frac{\text{sgn}(1-\omega )+\text{sgn}(\omega +1)}{2} & x\in \mathbb{C} & \infty & 2 \\ 8 & F(x) & -\frac{1}{2} i \pi e^{-\pi ^2 \omega ^2} \text{sgn}(\omega ) & x\in \mathbb{C} & \infty & \frac{\sqrt{\pi }}{2} \\ \end{array}$$
The remainder of this question illustrates some of the nested Fourier series representations of $f(x)$ for some of the example functions in Table (1) above.
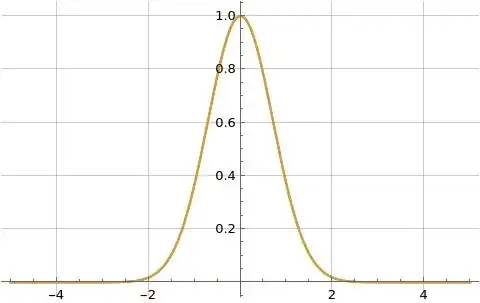
Figures (1) to (3) below illustrate formula (11) for $f(x)=e^{-x^2}$ in orange overlaid on the blue reference function $f(x)$ where $F(\omega)=\sqrt{\pi} e^{-\pi^2 \omega^2}$ and formula (11) is evaluated at $f=4$ and $N=10$.
Figure (1): Illustration of formula (11) for $f(x)=e^{-x^2}$ in orange overlaid on the blue reference function $f(x)$
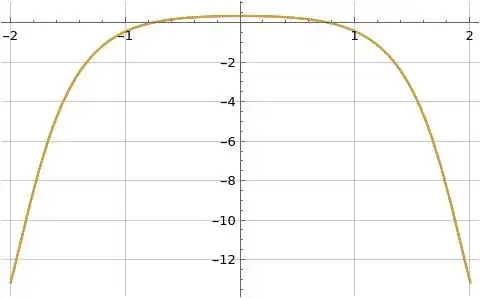
Figure (2): Illustration of real part of formula (11) for $f(1+i t)$ in orange overlaid on the blue reference function $\Re(f(1+i t))$ where $f(x)=e^{-x^2}$
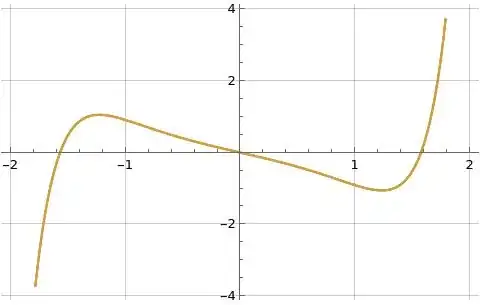
Figure (3): Illustration of imaginary part of formula (11) for $f(1+i t)$ in orange overlaid on the blue reference function $\Im(f(1+i t))$ where $f(x)=e^{-x^2}$
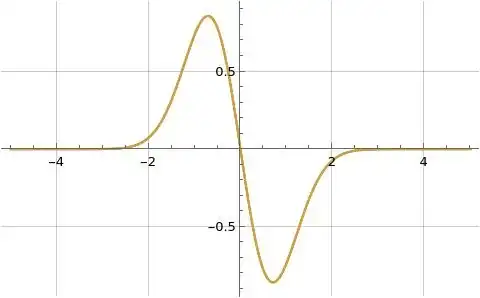
Figure (4) below illustrates formula (12) for $f(x)=-2 x e^{-x^2}$ in orange overlaid on the blue reference function $f(x)$ where $F(\omega)=2 i \pi^{3/2} \omega e^{-\pi ^2 \omega ^2}$ and formula (12) is evaluated at $f=4$ and $N=10$.
Figure (4): Illustration of formula (12) for $f(x)=-2 x e^{-x^2}$ in orange overlaid on the blue reference function $f(x)$
Figure (5) below illustrates formula (11) for $f(x)=e^{-|x|}$ in orange overlaid on the blue reference function $f(x)$ where $F(\omega)=\frac{2}{4 \pi^2 \omega^2+1}$ and formula (11) is evaluated at $f=4$ and $N=10$.
Figure (5): Illustration of formula (11) for $f(x)=e^{-|x|}$ in orange overlaid on the blue reference function $f(x)$