0

So I am doing an introductory course on theory of real functions and am having hard time thinking of examples.

I know various theorems and can tell whether or not a continuous function with specific details exists. However, I would want to know how do experts come up with examples so quickly?

Consider this question:

Does there exist a continuous function $f:\mathbb R\to\mathbb R$ such that $f((0,1))=[0,1]?$

Initially, I was under the impression that pre-image of a closed set must be closed and thus, no such function exists. Later, I realized that it is not at all necessary to have $(0,1)= f^{-1}([0,1])$, rather it's possible that $(0,1)\subset f^{-1}([0,1])$.

For the sake of clarity of notation: $f^{-1}([0,1])=\{x\in\mathbb R \text{ such that } f(x)\in[0,1]\}\tag*{}$

I am kind of sure that such a function (as described in the question) exists, however, I can't think of examples in my mind.

I did the same question a while back with different intervals. Continuous $f:\mathbb R\to\mathbb R$ such that $f((-1,1))=[-1,1]$. I didn't have to think much and I came up with $f(x)=\sin(\pi x)$ which works.

If I translate and scale everything, I think I have $g((-1,1))=[-1,1]$ for: $$\displaystyle g(x)=\frac{\sin(\pi(2x-1))+1}{2}$$

I hope this example is correct. Is there any simpler example (like ones which I can quickly produce in a exam setting...)?

Update:

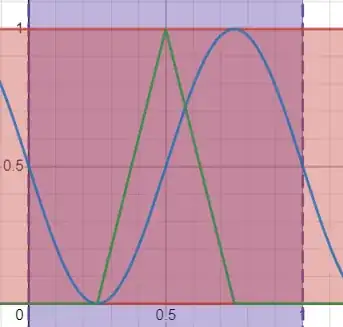
User localshop suggested that we can partition the interval $(0,1)$ and construct an isolated (half-period of) a triangle wave.

$$h(x)=\begin{cases}0 &\text{if $x\leq 0.25$}\\ 4x-1&\text{if $0.25\leq x\leq 0.5$}\\ -4x+3&\text{if $0.5\leq x\leq 0.75$}\\ 0 &\text{if $x\geq 0.75$}\end{cases}$$

Thanks to Desmos. Here's what the graphs looks like in the region $(0,1)\times [0,1]$:

enter image description here
[$h(x)$ in green and $g(x)$ in blue]

Nothing special
  • 1,992
  • 2
    If $f$ were increasing, then the image of the open interval would be open, so some change of sign of slope of $f$ is necessary (or at least making slope zero) , hence your examples are likely as simple as it gets – Bartosz Malman Jan 07 '24 at 16:31
  • 1
    Depending on what you call simpler and what you want to do with the function, you could consider $x\mapsto 0,x\in\left(0,\frac14\right)\cup\left(\frac34,1\right),x\mapsto 4x-1,x\in\left[\frac14,\frac12\right),x\mapsto -4x+3,x\in\left[\frac12,\frac34\right]$. This is not differentiable everywhere, however. –  Jan 07 '24 at 16:33
  • Why not f(x)=x ? – Lourrran Jan 07 '24 at 16:42
  • @Lourrran because then $f((0,1))=(0,1)\neq[0,1]$ – Lorago Jan 07 '24 at 16:43
  • @localshop I looked up your function on Desmos, it seems to work. How did you come up with it? You partitioned $(0,1)$ into disjoint intervals $(0,0.25)\cup [0.25, 0.5)\cup[0.5, 0.75]\cup (0.75, 1)$ and came up with linear functions for each while maintaining continuity at the points $0.25$, $0.50$ and $0.75$... Since the question wanted $f:\mathbb R\to \mathbb R$, we can define $f(x)=0$ for rest of the points. – Nothing special Jan 07 '24 at 16:51
  • If should also be possible to find an cubic polynomial with the desired property, but I don't have an explicit one right now – Lorago Jan 07 '24 at 16:56
  • 1
    @Nothingspecial ... you more or less described the process - it is an isolated (half-peroid of a) triangle wave (https://en.wikipedia.org/wiki/Triangle_wave). These are occasionally useful for constructing (counter-)examples in analysis. And yes, outside of $(0,1)$ the function I had in mind vanishes. –  Jan 07 '24 at 17:12
  • @Lorago See LeeMosher's answer, they found a cubic polynomial which works. – Nothing special Jan 07 '24 at 22:47
  • 1
    You could also appropriately modify any (non-zero) compactly supported smooth function on $\mathbb{R}$ to get something similar to the triangle wave construction – Lorago Jan 07 '24 at 22:55

2 Answers2

2

If you do a precalculus analysis of the graph of the function $g(x)=x^3-3x$ you'll see that $$g(-\sqrt{3},+\sqrt{3}) = [-2,+2] $$ Now just linearly scale and shift the $x$ and $y$ axes to adjust the domain and range: $$f(x) = a + b g(cx + d) $$ Letting $c = 2 \sqrt{3}$ and $d=-\sqrt{3}$, the function $cx+d$ takes $(0,1)$ to $(-\sqrt{3},\sqrt{3})$.

Then $g$ takes $(-\sqrt{3},+\sqrt{3})$ to $[-2,+2]$

And finally, letting $a=\frac{1}{2}$ and $b=\frac{1}{4}$, the function $a+by$ takes the interval $[-2,2]$ to the interval $[0,1]$.

Lee Mosher
  • 120,280
1

Much simpler than that you won't be able to get. A slight bit simpler could be for instance $$ f(x) = \begin{cases} 0 & \text{if } \quad x \leq 1/4 \\ 2x - \frac{1}{2} & \text{if } \quad 1/4 < x < 3/4 \\ 1 & \text{if } \quad 3/4 \leq x \end{cases} $$ where you only partition the interval in $3$ parts instead of $4$.

Essentially: if you want such a function, you will need a function that maps some closed interval $[a,b] \subsetneq [0,1]$ to $[0,1]$ such that the rest of the function stays inside $[0,1]$ on $(0,1)$.

soggycornflakes
  • 797
  • This works... Desmos Graph. So it was not necessary to choose $\left[\frac{1}{4}, \frac{3}{4}\right]$ as the middle part... – Nothing special Jan 07 '24 at 18:07
  • 1
    No, exactly. You can choose any closed interval for your 'middle part'. – soggycornflakes Jan 07 '24 at 18:08
  • Perhaps a better way of phrasing the last sentence in my response: you could characterize functions $f$ that satisfy $f(0,1) = [0,1]$ as functions such that $f([0,1]) = [0,1]$ and for which there are $a,b \in (0,1)$ such that $f(a) = 0, f(b) = 1$. – soggycornflakes Jan 07 '24 at 18:10
  • I think I have got a general outline on how to find examples... Given a set of conditions, first I'll try to see that if they are incompatible with any theorem or not... Following that I will partition the required interval and try to put linear functions for each part which do the work. I will wait a few more days before accepting your answer :) – Nothing special Jan 07 '24 at 18:13
  • 1
    Of course this sort of solution is heavily dependent on the conditions you are imposing. You'll have to grow a little intuition behind how functions behave on intervals to solve general questions. I wish you the best of luck! – soggycornflakes Jan 07 '24 at 18:16