If $(a,b,c)$ are the sides of a triangle and $x \ge 1$, what is the probability that $a+b > cx$?

Question

I am trying to generalize the triangle inequality in probabilistic terms. Assume that the vertices are uniformly distributed around the circumference of a fixed circle. In this question it was proved that if $(a,b,c)$ are the sides of a triangle than the probability that geometric mean of any two sides is greater than the third side i.e. $P\left(\sqrt{ab} > c\right) = \frac{2}{5}$. Since $a+b > 2\sqrt{ab}$, it implies that probability that $P(a+b > 2c) > \frac{2}{5}$. In general, we can ask:

Question: If $(a,b,c)$ are the sides of a triangle and $x \ge 1$, what is the probability that $a+b > cx$?

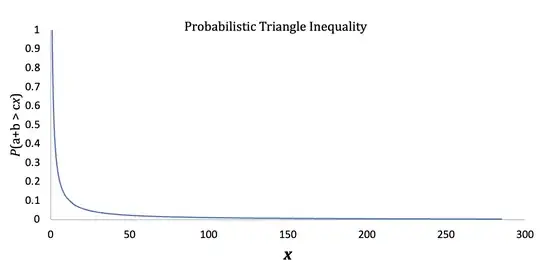
Experimental data: For each $x$ between $1$ and $300$ and at intervals of $0.01$, I ran $10^7$ trails and obtained an estimate of the complimentary cumulative distribution function $P(a+b > cx)$ plotted below.

Intuitively the graph makes sense since for $x=1$ the standard triangle inequality implies that the probability is $1$; and as $x \to \infty$ the probability must approach $0$ since we can make the sides $a$ and $b$ arbitrarily large and $c$ arbitrarily small. On fitting different models to this data, the best fit with an $R^2$ value of $0.999996$ and a standard error of $0.00019$ was given by

$$ P(a+b > cx) = \frac{6}{5x+1} $$

Update 9-Jan-2024: In my code, I was sorting the angles before getting the side length due to which order of the side cannot be interchanged. Under this restricted conditions, the above model could be the probability, however in unconditional case were the sides can be interchanged and vertices are uniformly distributed, the answer by @Empy2 is correct.

Equivalence with the Basel's Problem: The series in the accepted answer is actually the Lengendre Chi function $\chi_2\left(\frac1{x}\right)$. Taking $x = 1$ and applying the fact that the sum of the reciprocal of odd squares is $3/4$-th the sum over the reciprocal of the squares of natural numbers we find that the probability that the sum of any two sides of a triangle is greater than than the third side is $\displaystyle \frac{6\zeta(2)}{\pi^2}$. Since this probability must be $1$ and the proof does not require the value of to be known in advance, it unexpectedly implies that:

The triangle inequality equivalent to $$ 1 + \frac{1}{2^2} + \frac{1}{3^2} + \cdots = \frac{\pi^2}{6} $$

I have changed the title to reflect this remarkable connection.

Related question: If $(a,b,c)$ are the sides of a triangle, is it true that probability that $a+b > c^{\frac{3}{c}}$ is $\zeta(2)-1$?

Answer 1

I have a formula for the probability, which for large $x$ is roughly $$\frac4{\pi^2}(\frac2x+\frac2{9x^3}+\frac2{25x^5}+\cdots)$$ The series continues in the same form up to at least the $x^{-11}$ term. There is an integral form at the end of this answer.

Solution:

The angles in the triangle are all twice the corresponding angles at the centre of the circle. So the trio of angles $(\alpha,\beta,\gamma)$ is equally distributed over the flat region in 3space with vertices $(\pi,0, 0),(0,\pi,0),(0,0,\pi)$.
The area of a triangle with sides $a,b,c$ and angles $\alpha,\beta,\gamma$ is $$\Delta=\frac12ab\sin\gamma=\frac12ca\sin\beta=\frac12bc\sin\alpha$$
So for example $a=\frac{abc}{2\Delta}\sin\alpha$, and the ratio we want is $$\frac{a+b}c=\frac{\sin\alpha+\sin\beta}{\sin\gamma}\\=\frac{2\sin\frac{\alpha+\beta}2\cos\frac{\alpha-\beta}2}{\sin(\alpha+\beta)}\\ =\frac{\cos\frac{\alpha-\beta}2}{\cos\frac{\alpha+\beta}2}$$
The region of interest is $0\le\alpha,0\le \beta,\alpha+\beta\le\pi$. Change variables to $$\theta=\frac{\alpha+\beta}2,\phi=\frac{\alpha-\beta}2$$
The region is now $$0\le\theta\le\pi/2,\\-\theta\le\phi\le\theta$$ with area $\pi^2/4$.
The ratio of interest is greater than $x$ when $$\cos\theta\lt\frac{\cos\phi}x$$
For a given $\phi$, Theta ranges over an interval of length $$\pi/2-\arccos(\frac{\cos\phi}x)\\=\arcsin(\frac{\cos\phi}x)$$
Integrate that over the region to give $$\frac4{\pi^2}\int^{\pi/2}_{-\pi/2}\arcsin(\frac{\cos\phi}x)d\phi$$
I used a series expansion in arcsine $x+\frac{x^3}6+\frac{3x^5}{40}+\cdots$ to get the series at the top.

Answer 2

The posted code is wrong. I've refactored/bugfixed it slightly and the asymptotic value is in fact $8 / \pi^2$. The issue with sorting angles is that $a$ will be too small compared to $c$ (compared to if $a, b, c$ were generated from uniformly selected points and not ordered themselves).

from math import pi
import numpy as np
k = 2 * np.pi
n = 10**5
x = 1.0
max = 50
inc = 0.5
just run n trials for each value of x instead
while x < max:
    success = 0
    for _ in range(1, n):
        # remove the sort
        angles = np.random.uniform(0, k, 3)
    vertices_x = np.cos(angles)
    vertices_y = np.sin(angles)

    vertices_x = np.append(vertices_x, vertices_x[0])
    vertices_y = np.append(vertices_y, vertices_y[0])

    x_diff = np.diff(vertices_x)
    y_diff = np.diff(vertices_y)
    side_lengths = np.sqrt(x_diff ** 2 + y_diff ** 2)

    a = side_lengths[0]
    b = side_lengths[1]
    c = side_lengths[2]

    if a + b &gt; x * c:
        success += 1

print(f'x: {x:.4f}'[:-1], f'x * P(x): {x * success / n:.10f}'[:-1], f'8/pi^2: {8 / pi ** 2}')

x += 0.5

Sample output:

x: 1.000 x * P(x): 0.999990000 8/pi^2: 0.8105694691387022
x: 1.500 x * P(x): 0.861450000 8/pi^2: 0.8105694691387022
x: 2.000 x * P(x): 0.830600000 8/pi^2: 0.8105694691387022
x: 2.500 x * P(x): 0.830900000 8/pi^2: 0.8105694691387022
x: 3.000 x * P(x): 0.825840000 8/pi^2: 0.8105694691387022
x: 3.500 x * P(x): 0.817775000 8/pi^2: 0.8105694691387022
x: 4.000 x * P(x): 0.818160000 8/pi^2: 0.8105694691387022
x: 4.500 x * P(x): 0.814860000 8/pi^2: 0.8105694691387022
x: 5.000 x * P(x): 0.818700000 8/pi^2: 0.8105694691387022
x: 5.500 x * P(x): 0.818895000 8/pi^2: 0.8105694691387022
x: 6.000 x * P(x): 0.804540000 8/pi^2: 0.8105694691387022
x: 6.500 x * P(x): 0.800540000 8/pi^2: 0.8105694691387022
x: 7.000 x * P(x): 0.809200000 8/pi^2: 0.8105694691387022
x: 7.500 x * P(x): 0.809550000 8/pi^2: 0.8105694691387022
x: 8.000 x * P(x): 0.808240000 8/pi^2: 0.8105694691387022
x: 8.500 x * P(x): 0.808520000 8/pi^2: 0.8105694691387022
x: 9.000 x * P(x): 0.815310000 8/pi^2: 0.8105694691387022
x: 9.500 x * P(x): 0.797240000 8/pi^2: 0.8105694691387022
x: 10.000 x * P(x): 0.815900000 8/pi^2: 0.8105694691387022
x: 10.500 x * P(x): 0.802200000 8/pi^2: 0.8105694691387022
x: 11.000 x * P(x): 0.827090000 8/pi^2: 0.8105694691387022
x: 11.500 x * P(x): 0.813280000 8/pi^2: 0.8105694691387022
x: 12.000 x * P(x): 0.818640000 8/pi^2: 0.8105694691387022
x: 12.500 x * P(x): 0.813875000 8/pi^2: 0.8105694691387022
x: 13.000 x * P(x): 0.815750000 8/pi^2: 0.8105694691387022
x: 13.500 x * P(x): 0.806895000 8/pi^2: 0.8105694691387022
x: 14.000 x * P(x): 0.832300000 8/pi^2: 0.8105694691387022
x: 14.500 x * P(x): 0.802865000 8/pi^2: 0.8105694691387022
x: 15.000 x * P(x): 0.823050000 8/pi^2: 0.8105694691387022
x: 15.500 x * P(x): 0.805225000 8/pi^2: 0.8105694691387022
x: 16.000 x * P(x): 0.816480000 8/pi^2: 0.8105694691387022
x: 16.500 x * P(x): 0.805035000 8/pi^2: 0.8105694691387022
x: 17.000 x * P(x): 0.801380000 8/pi^2: 0.8105694691387022
```

Answer 3

I make a connection with a famous problem the disk triangle picking see

Dtp

Note that the probability decrease as the graph of the Op .