Stochastic Calculus : Dangers of Incorrectly Calculating Derivatives

Question

I am trying to understand the importance of Ito's Lemma in Stochastic Calculus.

When I learn about some mathematical technique for the first time, I always like to ask questions such as : "Is this complicated approach truly necessary - and what happens if I were to incorrectly persist with a simpler approach? How much trouble can I land myself into by persisting within the incorrect and simpler approach? Are there some situations where this is more of a problem compared to other situations where this might be less of a problem?"

Part 1: For example, consider the following equation:

$$f(t, B_t) = X_t = \mu t + \sigma \log(B_t)$$

Where:

• $X_t$ is the stochastic process
• $\mu$ is the drift term
• $\sigma$ is the volatility term
• $B_t$ is a geometric Brownian motion.

When it comes to taking the derivative of this equation, there are 3 approaches that come to mind:

Approach 1: Basic Differencing

We can do this by simulating $X_t$ and evaluates consecutive differences: $$df(t, B_t) = f(t, B_t) - f(t_{-1}, B_{t-1}) $$ or $$dX_t = X_t - X_{t-1} $$

Approach 2: Basic Calculus (Incorrect):

If this was a basic calculus derivative, for some generic function $f(x,y)$, I could use chain rule to determine:

$$\frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}$$

$$df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$$

Thus, applying the logic of basic calculus incorrectly to stochastic calculus, I would incorrectly determine that:

$$f(t, B_t) = \mu t + \sigma \log(B_t)$$

$$df(t, B_t) = \frac{\partial}{\partial t} f(t,B_t) dt + \frac{\partial}{\partial B_t} f(t, B_t) dB_t$$

$$df(t, B_t) = \mu dt + \sigma \left(\frac{1}{B_t}\right) dB_t$$

Approach 3: Ito's Calculus (Correct):

Just to recap, in a Taylor Expansion of a non-stochastic function, we can show that a first order Taylor Expansion of a function equals to its first derivative (in limit), since all other higher order terms are negligible:

$$f(x + \Delta x) = f(x) + (\Delta x) f'(x) + \frac{(\Delta x)^2}{2} f''(x) + ... $$ $$(\Delta x) f'(x) = f(x + \Delta x) - f(x) - 0.5(\Delta x)^2 f''(x) + ... $$ $$f'(x) = \frac{f(x + \Delta x) - f(x)}{\Delta x} - 0.5 \Delta x f''(x) + ...$$

$$\lim_{\Delta x \to 0} f'(x) = \lim_{\Delta x \to 0} \left( \frac{f(x + \Delta x) - f(x)}{\Delta x} \right) - \lim_{\Delta x \to 0} \left(0.5 \Delta x f''(x)\right) + \lim_{\Delta x \to 0} (....) $$

$$f'(x) = f'(x) - 0$$

$$f'(x) = f'(x) $$

However, this is not true in the Taylor Expansion of a stochastic function:

$$df = \left(\frac{dB_t}{dt} f'(B_t)\right) dt$$

Since the Brownian Motion is not smooth and not differentiable in any interval (i.e. if you zoom into a very small part, there is still "more Brownian Motion" happening). Thus, $dB_t$ is defined, but $\frac{dB_t}{dt}$ is not defined.

In the non-stochastic case, we could have written the Taylor Series this way with all higher order terms dropping off:

$$\Delta f = f(x + \Delta x) - f(x) = (\Delta x) f'(x) + \frac{(\Delta x)^2}{2} f''(x) + ... $$

But, for some stochastic function of a Brownian Motion $f(B_t)$, if we were to write the same Taylor Series:

$$\Delta f = f(B_t + \Delta B_t) - f(B_t) = (\Delta B_t) f'(B_t) + \frac{(\Delta B_t)^2}{2} f''(B_t) + ...$$

We know that $\Delta B_t$ (i.e. two differences in a Brownian Motion) is equal to a Weiner Process, i.e.

$$B_{t+s} - B_s = W_t \sim N(0, t)$$ $$\Delta B_t = B_{t+\Delta t} - B_t = W_t \sim N(0, \Delta t)$$ $$\text{Var}(\Delta B_t^2) = E(\Delta B_t^2) - E(\Delta B_t)^2 = \Delta t - 0 = \Delta t $$ $$E(\Delta B_t^2) = \Delta t $$

Going back to the Taylor Series of the stochastic function, we can now make this replacement for $\Delta t$ using the Expected Value:

$$\Delta f = f(B_t + \Delta B_t) - f(B_t) = (\Delta B_t) f'(B_t) + \frac{(\Delta t)^2}{2} f''(B_t) + ...$$

Now (for some reason that I don't understand), the second order term is not negligible anymore. Using this information, we can now formally write Ito's Lemma as :

$$df(t, B_t) = \frac{\partial f}{\partial t} dt + \frac{\partial f}{\partial B_t} dB_t + \frac{1}{2} \frac{\partial^2 f}{\partial B_t^2} (dB_t)^2$$

Now, going back to our original problem, for the function $f(t, B_t) = X_t = \mu t + \sigma \log(B_t)$, we can write:

• $\frac{\partial f}{\partial t} = \mu$
• $\frac{\partial f}{\partial B_t} = \frac{\sigma}{B_t}$
• $\frac{\partial^2 f}{\partial B_t^2} = -\frac{\sigma}{B_t^2}$

Thus, the final answer is:

$$df(t, B_t) = \mu dt + \frac{\sigma}{B_t} dB_t - \frac{1}{2} \frac{\sigma}{B_t ^2} dt$$ Note that $ Var(B_t) = E(B_t^2) - E(B_t)^2 = t - (0)^2 = t$

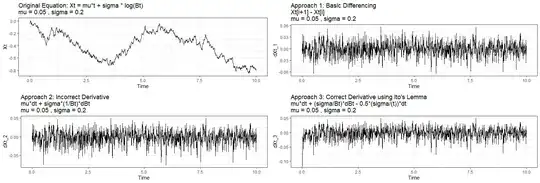
Part 2: Looking at Part 1 (provided I have done everything correctly), it is not immediately clear to me what are the "dangers" of incorrectly calculating the derivative (i.e. how much more "wrong" would the incorrect approach be compared to the correct approach). To get a better understanding of this, I tried to make a computer simulation to look at this (using the R programming language):

library(ggplot2)
set.seed(123)
parameters
n <- 1000
dt <- 0.01
mu <- 0.05
sigma <- 0.2
t <- seq(0, (n-1)dt, dt)
Bt <- exp(cumsum(rnorm(n, 0, sqrt(dt))))
Xt <- mu  t + sigma * log(Bt)
Original stochastic process: Xt = mut + sigma  log(Bt)
p1 <- ggplot(data.frame(Time = t, Xt = Xt), aes(Time, Xt)) +
    geom_line() +
    labs(title = paste("Original Equation: Xt = mut + sigma  log(Bt)\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
Approach 1: Basic Differencing
dXt_1 = Xt[i+1] - Xt[i]
dXt_1 <- c(0, diff(Xt))
p2 <- ggplot(data.frame(Time = t, dXt_1 = dXt_1), aes(Time, dXt_1)) +
    geom_line() +
    labs(title = paste("Approach 1: Basic Differencing\nXt[i+1] - Xt[i]\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
Approach 2: Incorrect Derivative using basic calculus
dXt_2 = mudt + sigma(1/Bt)*dBt
dBt <- c(0, diff(Bt))
dXt_2 <- mu * dt + sigma * (1 / Bt) * dBt
p3 <- ggplot(data.frame(Time = t, dXt_2 = dXt_2), aes(Time, dXt_2)) +
    geom_line() +
    labs(title = paste("Approach 2: Incorrect Derivative\nmudt + sigma(1/Bt)*dBt\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
Approach 3: Correct Derivative using Ito's Lemma
dXt_3 = mudt + (sigma/Bt)dBt - 0.5(sigma/(Bt^2))dt
dXt_3 <- mu * dt + (sigma / Bt) * dBt - 0.5 * (sigma / (t)) * dt
p4 <- ggplot(data.frame(Time = t, dXt_3 = dXt_3), aes(Time, dXt_3)) +
    geom_line() +
    labs(title = paste("Approach 3: Correct Derivative using Ito's Lemma\nmudt + (sigma/Bt)dBt - 0.5(sigma/(t))dt\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()

In the above graphs, the results of all 3 approaches look quite similar to one another.

I then compared the absolute differences between Approach 1 and Approach 3, and between Approach 2 and Approach 3:

abs_diff_1_3 <- abs(dXt_1 - dXt_3)
abs_diff_2_3 <- abs(dXt_2 - dXt_3)
p5 <- ggplot(data.frame(Time = t, AbsDiff = abs_diff_1_3), aes(Time, AbsDiff)) +
    geom_line() +
    labs(title = "Absolute Difference between Approach 1 and 3") +
    theme_bw()
p6 <- ggplot(data.frame(Time = t, AbsDiff = abs_diff_2_3), aes(Time, AbsDiff)) +
    geom_line() +
    labs(title = "Absolute Difference between Approach 2 and 3") +
    theme_bw()

Again, all results look quite similar to one another.

My Question: Based on this exercise, it seems like whether you take the correct derivative (via Ito's Lemma) or the incorrect derivative (basic calculus), the final answer looks very similar. Thus, is Ito's Lemma more of a theoretical consideration with little added value compared to the incorrect derivative? Or perhaps there are much bigger differences for the derivatives of other functions (and perhaps for stochastic integrals)?

Thus, for stochastic functions, is there any "real danger" in incorrectly calculating their derivatives and integrals using basic calculus methods?

Thanks!

Note: The one thing that comes to mind is perhaps Ito Calculus is really needed when you need to take the derivative or integral of a stochastic function in an intermediate step for some math problem (e.g. first passage time). In such cases, perhaps the "danger" of propagating an incorrect result is much higher compared to these basic simulations.

References:

• https://ocw.mit.edu/courses/18-s096-topics-in-mathematics-with-applications-in-finance-fall-2013/ef2c66c8079ba656210ad1fd4a5e2fa8_MIT18_S096F13_lecnote18.pdf

• Distribution of Brownian Motion squared

• https://stats.libretexts.org/Bookshelves/Probability_Theory/Probability_Mathematical_Statistics_and_Stochastic_Processes_%28Siegrist%29/18%3A_Brownian_Motion/18.01%3A_Standard_Brownian_Motion

Answer 1

There are a few issues at hand.

First, your code doesn't match your post: where you wrote

dXt_3 <- mu * dt + (sigma / Bt) * dBt - 0.5 * (sigma / (t)) * dt

I think you probably meant

dXt_3 <- mu * dt + (sigma / Bt) * dBt - 0.5 * (sigma / (Bt ^ 2)) * dt.

In which case the absolute difference between the two can be drastic. (Run it yourself!)

More imporantly, is that at the top you declare that $B_t$ is a geometric Brownian motion, and in the code you do in fact approximate Bt $\approx \exp(W_t)$ for some standard Brownian motion $W_t$. However, in the Ito calculus section, you seem to compute $(dB_t)^2 = t$ as if $B_t$ were standard BM as well.

I'm going to assume that you meant that $B_t = \exp(W_t)$ for a standard BM $W_t$ (as in the simulation), in which case $$ X_t = \mu t + \sigma W_t $$ and both "standard calculus" and the Ito lemma give $$ dX_t = \mu dt + \sigma dW_t $$ since the second derivative of $x \mapsto x$ vanishes. (As an aside, if you want to understand where the Ito lemma picks up the second derivative, it is because $\lim_{n \to \infty} \sum_i^n (W_{(i + 1)/n} - W_{i/n})^2 \neq 0$; now look at the Taylor expansion of $f(t, W_t)$.

In fact, $B_t = \exp(W_t)$ satisfies the SDE $$ dB_t = \frac{B_t}{2}dt + B_tdW_t $$ so you can check that if you substitute this alongside $(dB_t)^2 = B_t^2$ (do you know how to compute this quadratic variation from the above SDE?) into your original formula $$ dX_t = \mu dt + \frac{\sigma}{B_t} dB_t + \frac{\sigma}{2B_t^2}dt $$ one does in fact get $$ dX_t = \mu dt + \sigma dW_t $$ as expected, so in this case the Ito lemma and standard calculus agree once we carry out the computation correctly. But this is misleading, since this is practically the only case where this happens.

Instead, let us pick another process such that the Ito formula and standard calculus disagree. Set $W_t$ to be a standard BM and $$ X_t = \mu t + \sigma W_t^3 $$ so that the standard calculus approach gives $$ dX_t = \mu dt + 3\sigma W_t^2 dW_t $$ and the Ito lemma yields $$ dX_t = (\mu + 3 \sigma W_t) dt + 3 \sigma W_t^2 dW_t. $$ Then, running the same code as you, but modified to this process, I get the following results.

library(ggplot2)
set.seed(1)
parameters
n <- 1000
dt <- 0.01
mu <- 0.05
sigma <- 0.2
t <- seq(0, (n-1)dt, dt)
Wt <- cumsum(rnorm(n, 0, sqrt(dt)))
Xt <- mu  t + sigma * (Wt ^ 3)
p1 <- ggplot(data.frame(Time = t, Xt = Xt), aes(Time, Xt)) +
    geom_line() +
    labs(title = paste("Original Equation: Xt = mut + sigma  Wt^3)\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
Approach 1: Basic Differencing
dXt_1 = Xt[i+1] - Xt[i]
dXt_1 <- c(0, diff(Xt))
p2 <- ggplot(data.frame(Time = t, dXt_1 = dXt_1), aes(Time, dXt_1)) +
    geom_line() +
    labs(title = paste("Approach 1: Basic Differencing\nXt[i+1] - Xt[i]\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
Approach 2: Incorrect Derivative using basic calculus
dWt <- c(0, diff(Wt))
dXt_2 <- mu * dt + 3 * sigma * (Wt ^ 2) * dWt
p3 <- ggplot(data.frame(Time = t, dXt_2 = dXt_2), aes(Time, dXt_2)) +
    geom_line() +
    labs(title = paste("Approach 2: Incorrect Derivative\nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
Approach 3: Correct Derivative using Ito's Lemma
dXt_3 <- mu * dt + 3 * sigma * (Wt ^ 2) * dWt + 3 * sigma * Wt * dt
p4 <- ggplot(data.frame(Time = t, dXt_3 = dXt_3), aes(Time, dXt_3)) +
    geom_line() +
    labs(title = paste("Approach 3: Correct Derivative using Ito's lemma \nmu =", mu, ", sigma =", sigma)) +
    theme_bw()
abs_diff_1_3 <- abs(dXt_1 - dXt_3)
abs_diff_2_3 <- abs(dXt_2 - dXt_3)
p5 <- ggplot(data.frame(Time = t, AbsDiff = abs_diff_1_3), aes(Time, AbsDiff)) +
    geom_line() +
    labs(title = "Absolute Difference between Approach 1 and 3") +
    theme_bw()
p6 <- ggplot(data.frame(Time = t, AbsDiff = abs_diff_2_3), aes(Time, AbsDiff)) +
    geom_line() +
    labs(title = "Absolute Difference between Approach 2 and 3") +
    theme_bw()

Do you still believe that Ito's lemma is just a theoretical exercise? In fact, note that the difference is $3\sigma W_tdt$, so we actually expect the error to grow as $t \to \infty$ in this case! If n = 10000 instead in the above code, we get the following error plot: