$2n$ objects of each of three kinds are given to two persons, so that each person gets $3n$ objects. Prove that this can be done in $3n^2 + 3n + 1$ways.
My attempt :
$x+y+z=3n$ and $0\le x,y,z\le 2n$
Number of solutions $= \binom {3n+2}{2}-3\binom {n+1}{2}=3n^2+3n+1$
Aliter:
$x+y+z=3n $ and $0\le x,y,z\le 2n$ $\iff n\le x+y\le 3n, 0\le x,y\le 2n$
Now plot the inequalities and count lattice points!! the required lattice points falls inside or boundaries of two squares and two triangles. $= 2\frac{(n+1)(n+2)}{2 }+2(n+1)^2-2(2n+1)-1= 3n^2+3n+1.$
Aliter:
If the first person gets $n − p (p\le\mathbb{N}_0)$ objects of the first kind, then the person can get $p$ to $2n$ objects of the second kind. The remaining ones are objects of the third kind. The sum is $\sum_{p=0}^{n}(2n+1-p)=(2n + 1)(n + 1) −\frac {n(n+1)}{2}$
If the first person gets $n + q (q\in\mathbb{N}) $objects of the first kind, then the person gets $0$to $(2n − q)$ objects of the second kind, since the person gets $3n$ objects altogether. The sum is $\sum_{q=1}^{n}(2n − q + 1)=n(2n + 1) − \frac {n(n+1)}{2}$ So total $=(2n+1)(n+1)+n(2n+1)−n(n+1)=3n^2+3n+1.$
I want clarification in following solution:
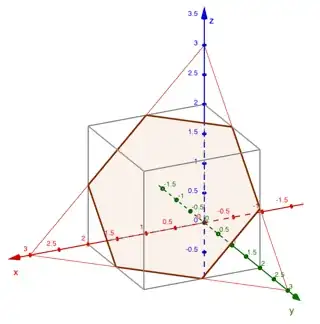
The result $3n^2+ 3n + 1 = (n + 1)^3 - n^3$ is striking and allows a geometrical interpretation. One person gets $x+y+z = 3n$ objects with $ 0 \le x, y, z \le 2n.$ These are triangular coordinates for an equilateral triangle with altitude $3n. x, y, z $ can be interpreted as lattice points (make a figure). The hexagon in the figure can be interpreted as the projection of the cube with edge $n + 1$ from which a cube of edge $n$ is subtracted. This solution is due to Martin Härterich, a gold medallist of the IMO 1987/89.