How to show naturality of the section when trying to prove gluing axiom for sheaf hom

Question

The question is to show that the sheaf Hom$(U):=\{$morphisms of sheaves $\mathcal{F}|_{U}\to \mathcal{G}|_{U}\}$ is indeed a sheaf, where $\mathcal{F}$ and $\mathcal{G}$ are fixed sheaves on the same topological space $X$.

The accepted answer of this post gives a mostly detailed answer, and looks mostly like what I attempted. The main difference between what is done there and what I did is that I proved locality axiom directly without using the fact that it is a presheaf of abelian groups, but I don't think that should make a big difference.

Now, the question. Fix an open set $U$ and an open cover $\cup_{i\in I}U_i$. Suppose we have sections $\alpha_i\in$ Hom$(U_i)$, and we want to obtain a global section on $U$. Refer to Step 2 of the answer linked above. The user constructs a map from each $\mathcal{F}(V)\to \mathcal{G}(V)$ for each open subset $V\subset U$, and claims that this is a global section, which when restricted appropriately gives us the sections we started with.

My issue with the above is that I am unable to prove that the global section obtained as such is indeed a morphism of sheaves $\mathcal{F}|_{U}\to \mathcal{G}|_{U}$.

In summary, I have a map of sheaves $\alpha: \mathcal{F}|_{U}\to \mathcal{G}|_{U}$ such that the following diagram commutes for every open subset $V\subset U$, and every $i\in I$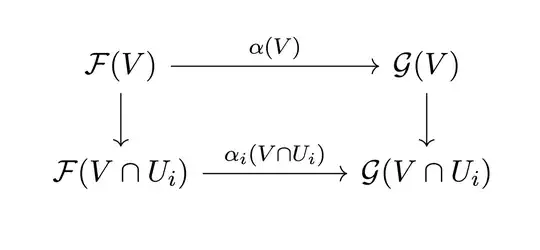$\alpha$" />

Wish to show that for all open subsets $B\subset A\subset U$, the following diagram commutes:

(All unmarked maps are sheaf restrictions)

Ok, let us assume for a moment that $\alpha$ as defined above is indeed a natural transformation. To conclude the argument, we need to show that for each $i$, $\alpha$ and $\alpha_i$ agree on all the open subsets of $U_i$. Let $Z\subset U_i$ be open. Assuming the diagrams above commute, we can get the following equality: $\alpha_i(Z)(\text{res}|_{Z}^{U_i})=\alpha(Z)(\text{res}|_{Z}^{U_i})$. Does this somehow enable us to conclude that $\alpha(Z)$ and $\alpha_i(Z)$ are the same on the entirety of $\mathcal{F}(Z)$?

Thanks in advance

Answer 1

Let $A$ and $B$ be open sets of $U$ such that $B\subset A$.$\newcommand{\f}{\mathcal F}\newcommand{\g}{\mathcal G}\newcommand{\a}{\alpha}$ Let $s\in\f(A)$. Then $\a(A)(s)$ is the unique section satisfying $$\a(A)(s)|_{A\cap U_i}=\a_i(A\cap U_i)(s|_{A \cap U_i})$$ for all $i$ (this is exactly your first diagram). We want to show that $$\a(A)(s)|_B=\a(B)(s|_B).$$ By the identity axiom, it suffices to show that these two sections agree on $B\cap U_i$ for all $i$. We have \begin{align} \a(A)(s)|_{B\cap U_i}&=(\a(A)(s)|_{A\cap U_i})|_{B\cap U_i}\\ &=(\a_i(A\cap U_i)(s|_{A \cap U_i}))|_{B\cap U_i}\\ \end{align} and since $\a_i$ is a morphism we get $$(\a_i(A\cap U_i)(s|_{A \cap U_i}))|_{B\cap U_i}=\a_i(B\cap U_i)(s|_{B\cap U_i})=\a(B)(s|_B)|_{B\cap U_i},$$ where the last equality is by the definition of $\alpha$ (it's good to have a diagram on your side). Thus $$\a(A)(s)|_{B\cap U_i}=\a(B)(s|_B)|_{B\cap U_i}$$ for all $i$ and we are done.