Odds in the dice game from Kakegurui Twin chapter 2

Question

In chapter 2 of the manga series Kakegurui Twins, there is a dice game named "Three-hit dice."

For those who have no idea what it is or don't want to read, I will briefly summarize the game rules here. In this game, a dealer wields the standard six-faced dice with faces 1,2,3 labelled "D" and faces 4,5,6 labelled "U." Two players write a three-letter sequence of "U"s and "D"s (for example, "UDU", "DDU", etc.) on a piece of paper and give to the dealer. The dealer will consecutively roll the dice and record each result "U" or "D" in a sequence. The player whose three-letter sequence first appears in the dealer's sequence will win the game. For example, suppose player A writes "UUD" and player B writes "DUD" and the dealer rolls "DDUD." In this case, player B wins because their sequence "DUD" appears in the dealer's sequence before player A's.

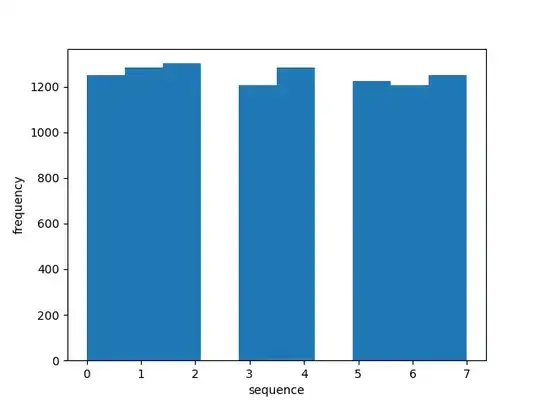
The manga claims that there are most-likely and least-likely three-letter sequences. The most-likely sequences are "UUD", "UDD", "DDU", and "DUU." The least-likely sequences are "DDD" and "UUU." I don't understand why this is the case. My naive intuition tells me that all $2^3=8$ three-letter sequences are equally likely to appear in the dealer's sequence. I confirmed it with my Python script:

import matplotlib.pyplot as plt
from random import randint
N = 10002
dice rolls are represented by a sequence of 0s and 1s
rolls = randint(0, 2**N - 1)
data = []
while rolls > 0:
    # extract a three-letter sequence
    data.append(rolls & 0b111)
    # delete the last result
    rolls >>= 1
plt.xlabel('sequence')
plt.ylabel('frequency')
plt.hist(data)
plt.show()

This histogram counts the number of occurrences for each three-letter sequence "DDD" (0), "DDU" (1), "DUD" (2), "DUU" (3), "UDD" (4), "UDU" (5), "UUD" (6), "UUU" (7). If the manga's claim is true, then I should see some kind of normal distribution in the histogram. The histogram clearly shows that each sequence are equally likely, so the manga might be wrong or there is something wrong with my simulation.

Also, the manga remarks that each three-letter sequence has a three-letter sequence it's likely to win against, like rock paper scissors. For example, "DUU" is more likely to appear first in the dealer's sequence before "UUD." I am not sure if it is true or false.

Answer 1

You have to be careful: it's not the probability of the occurrence of a dice you want to minimize, but it's time to show up the first time, i.e. the expected number of throws.

Indeed what you write is true: all sequences of symbols have the same probability a priori, but the average time it takes to reach one differs.

For example, if you were looking for a DDD but you throw DDU you need at least 3 more throws to possibly reach it, whereas if your choice would have been DUD just one more throw is needed. Basically you need to take into account also "recovering" from a bad throw.

Since your dice is basically a coin, following this answer you can find that the expected number of tosses for DDD is 14, and the number for UUD can be calculated analogously to that answer and you obtain just 8.

---

The 8 comes from the equation: $$x=\frac12(x+1)+\frac14(x+2)+\frac14\cdot (2+2)$$