4

How to find the derivative of $\sqrt{x^{2}+4+3(x+\operatorname{sgn}(x))}$. That is find $\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+4+3(x+\operatorname{sgn}(x))})$. Now we clearly know that $\operatorname{sgn}(x)$ is a piecewise function. We know that $\operatorname{sgn}(x)=\frac{|x|}{x}$ when $x\neq0$ and $0$ when $x=0$. Therefore when $x>0$ then the value of $\frac{|x|}{x}$ is $1$. When $x<0$ then the value of $\frac{|x|}{x}$ is $-1$. Now let's take cases.

Case-1): When $\operatorname{sgn}(x)=1$, then $\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+4+3x+3\operatorname{sgn}(x)})=\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+7+3x})=\frac{1}{2\sqrt{x^{2}+3x+7}}(2x+3)$.

Case-2): When $\operatorname{sgn}(x)=0$, then $\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+4+3x+3\operatorname{sgn}(x)})=\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{4})=0$.

Case-3): When $\operatorname{sgn}(x)=-1$, then $\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+4+3x+3\operatorname{sgn}(x)})=\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+3x+1})=\frac{1}{2\sqrt{x^{2}+3x+1}}(2x+3)$.

So, we can clearly see that $3$ different results are occuring for $\frac{\mathrm{d}}{\mathrm{d}x}(\sqrt{x^{2}+4+3(x+\operatorname{sgn}(x))}$. But I want to know that is my process correct? Are $3$ different results possible? Please do let me know.

PrincessEev
  • 43,815
Syamaprasad Chakrabarti
  • 1,269
  • 3
    Case 1 and 3 are correct (for case 3, you should first calculate for which negative $x$s your function $f$ is defined). Case 2 is wrong: $f$ is not differentiable at $0$, it is not even continuous. Its left and right limit are distinct, and distinct from $f(0)$. – Anne Bauval Dec 17 '23 at 23:07
  • Yes you are correct@AnneBauval. In case-2 f is not differentiable at 0, it is not even continuous. But here I am having a doubt. That is $sgn(x)=0$ only when $x=0$. Generally we take into consideration left and right handed limits only for the questions of continuity and differentiability. But this question is from diiferentiation. Please clear my doubt. – Syamaprasad Chakrabarti Dec 18 '23 at 08:43
  • "Generally we take into consideration left and right handed limits only for the questions of continuity and differentiability." Indeed! "But this question is from diiferentiation" Precisely! so this question belongs to the "general" case of your previous sentence. And you agreed that at $0$, $f$ is not continuous hence not differentiable. So what is your "doubt"? – Anne Bauval Dec 18 '23 at 11:18
  • No, actually I was getting $f'(0)=0$. And since you were saying that f is not continuous and differentiable at $0$ so I thought that my derivative was incorrect in case-2.@AnneBauval – Syamaprasad Chakrabarti Dec 18 '23 at 11:46
  • Indeed, as told in my first comment above, your case 2 is necessarily incorrect since $f'(0)$ does not exist. Actually your calculation is doubly wrong: 1)$f'(0)$ is not $g'(0)$ where $g(x):=\sqrt{x^{2}+4+3x+3\cdot0}$, because $f(x)=g(x)$ only for $x=0$, not for $x$ close to $0$. 2) $g'(0)\ne h'(0)$ where $h(x):=\sqrt4$, because $g(x)=h(x)$ only for $x=0$, not for $x$ close to $0$. – Anne Bauval Dec 18 '23 at 12:41
  • Note that the logic you used in case 2 to arrive at a derivative of $0$ can equally well show that the derivative of any function, at any point in its domain, is $0$. If we have some function $f(x)$ which is defined at a point $x = a$, Then the derivative at $a$ would be, by your logic, $f'(a) = \frac{d}{dx}(f(a)) = 0$ since $f(a)$ doesn't depend on $x$. But of course this is false, because $f'(a)$ does not depend just on the value of $f(a)$, but on the values of $f(x)$ for $x$ near $a$. – Paul Sinclair Dec 20 '23 at 18:04

2 Answers2

7

I would always be wary about taking the derivative at a single point, unless you know for sure the function is differentiable with continuous derivative ($\mathcal{C}^1$) around that point. Otherwise, issues might arise. Consider the contrived case of $$ f(x) = \begin{cases} 1, & x = 0 \\ 0, & x \ne 0 \end{cases} $$ where the derivative wouldn't even exist at $x=0$, but if you take the derivative of each "piece" of the function you would just naively conclude $f' \equiv 0$ everywhere. But you can see the issues arise via a number of techniques, including the limit definition of the derivative: $$ f'(\xi) := \lim_{x \to \xi} \frac{f(x) - f(\xi)}{x-\xi} \equiv \lim_{h\to 0} \frac{f(\xi+h) - f(\xi)}{h} $$ Some enlightening examples are here.

Thanks to the definition of $\newcommand{\sign}{\operatorname{sign}} \sign(x)$, then, your function - let's call it $f$ - technically has three pieces to be concerned with: $$ f(x) := \begin{cases} \sqrt{x^{2}+3x+7}, & \sign(x) =1 \text{; i.e., } x > 0 \\ \sqrt{x^{2}+3x+4}, & \sign(x) =0 \text{; i.e., } x = 0 \\ \sqrt{x^{2}+3x+1}, & \sign(x) =-1 \text{; i.e., } x < 0 \end{cases}$$

Graphically, $f$ has graph looking like this, each color representing one "case" above:

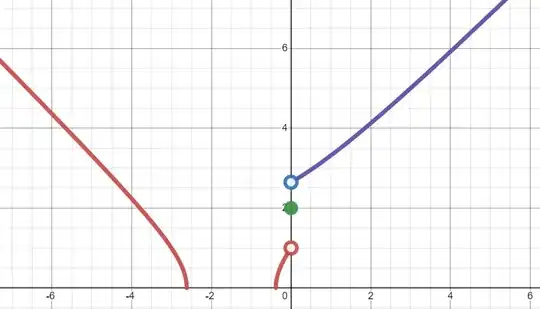
enter image description here

Notice how $f$ isn't even defined when $x^2+3x+1<0$, i.e. when $$ x \in \left( \frac{-3 - \sqrt 5}{2} , \frac{-3 + \sqrt 5}{2} \right) $$ so another concern of problems of this type to be wary of is when your derivative is defined for functions not even in the domain of $f$. I remember getting tripped on a problem of this type once, where we sought $f'$ for $f(x) := \ln(\ln(\sin(x)))$, the issue being $f$ isn't defined for any real number.

This isn't an issue for your problem, since your answer implicitly incorporates that, but I figured it worth noting in the general case.

Anyhow, the graph makes it clear that $f'$ doesn't exist at $x=0$: it isn't even continuous there. This can be seen from the limit definition, if you please. Essentially, you have

  • $\sqrt{x^2+3x+1} \xrightarrow{x \to 0^-} 1$ on the left branch
  • $\sqrt{x^2+3x+7} \xrightarrow{x \to 0^+} \sqrt 7$ on the right branch
  • $f(0)=2$

so the limit doesn't exist, you do not have continuity, and hence do not have differentiability.

In principle, can a piecewise-defined function have a (nontrivial) piecewise-defined derivative, though? Sure, that's not an issue by any means, and sometimes is even an important thing to have (such as in the implementation of splines). A very simple example is $$ f(x) := \begin{cases} x^2, & x \ge 0 \\ 0, & x < 0 \end{cases} $$ Clearly, $f'$ is $2x$ for $x > 0$ and $0$ for $x<0$, and it is not hard to see from the limit definition that $f'(0) = 0$, ensuring that $f$ is differentiable despite being piecewise.

PrincessEev
  • 43,815
0

First of all, if a function (defined in a neighborhood of $a$) is differentiable at $a$, then it is continuous at $a$. Thus, if you have a noncontinuous function at $a$, trying to compute the derivative is moot.

Now, if the function is continuous at $a$ and differentiable in a neighborhood of $a$ except, possibly at $a$, two cases are possible:

  1. the limit of $f'$ for $x\to a$ exists finite;
  2. the limit of $f'$ for $x\to a$ doesn't exist or is infinite.

In the first case, l'Hôpital's theorem allows you to say that $$ f'(a)=\lim_{x\to a}f'(x) $$ In the second case the derivative at $a$ may still exist. For instance $$ f(x)=\begin{cases} x^2\sin(1/x) & x\ne0 \\[6px] 0 & x=0 \end{cases} $$ where the limit of the derivative for $x\to0$ doesn't exist, but the function is differentiable at $x$.

You see that continuity at $a$ is the main aspect to check. In your case, the fact that $\operatorname{sgn}$ isn't continuous at $0$ shows that we need to check continuity of $f$. Since we have $$ f(x)=\begin{cases} \sqrt{x^{2}+4+3(x+1)} & x>0 \\[6px] 2 & x=0 \\[6px] \sqrt{x^{2}+4+3(x-1)} & x>0 \end{cases} $$ we clearly see that $f$ isn't continuous at $0$, so we're done: the derivative cannot exist.

A different example where one can compute the derivative at a point as a limit. Consider $$ f(x)=\begin{cases} \dfrac{e^x-1}{x} & x\ne0 \\[6px] 1 & x=0 \end{cases} $$ For $x\ne0$ we clearly have $$ f'(x)=\frac{xe^x-e^x+1}{x^2} $$ and we see that, using l'Hôpital, $$ \lim_{x\to0}f'(x)=\lim_{x\to0}\frac{xe^x}{2x}=\frac{1}{2} $$ so we can state that $f'(0)=1/2$.

egreg
  • 238,574