Here is an abstract algebra problem :
Solve the equation (in $ℚ[x]$) : $$f(x)(2x^3 + 3x^2 + 7x + 1) + g(x)(5x^4 + x + 1) = x + 3$$
From your comments, I tried to apply extended euclidean algo but it ends up with completely unlikely reminders and quotient. Can you please tell me what I'm doing wrong before I continue with these terrible calculations ?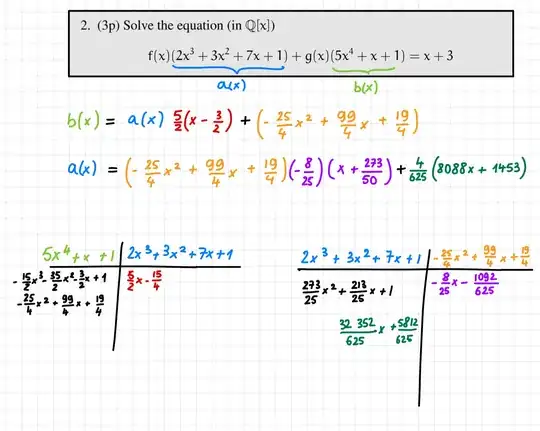
Thanks in advance.