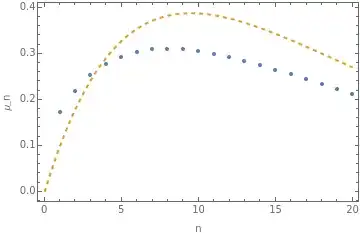
Let $(X_i)_{i\geq 0}$ be i.i.d. nonnegative random variables with continuous density function $f$. Let \begin{align} \mu_n = \mathbb{E}[X_{(n)}-X_{(n-1)}] \end{align} be the expected difference between the largest and second largest of the first $n$ random variables.
Question: Can we show that $\mu_n$ is decreasing in $n$?
We can assume the density $f$ to be decreasing for $x>0$ and the mean of the order statistics to be well-defined; in particular, assume $\mathbb{E}[X_i]<\infty$.
Edit: My intuition tells me that $\mu_n$ is generally decreasing in $n$, but I have been unable to prove it. I am more interested in simple conditions under which the result is true, rather than a specific counterexample where it is not.