Let $P(x,y)$ be any point and let $\rho$ and $\alpha$ be its polar coordinates. We have \begin{align*} x &= \rho\cos\alpha \\ y &= \rho\sin\alpha \end{align*} the point $P'(x',y')$, image of $P$ in a counterclockwise rotation of an angle $\theta$, has polar coordinates $(\rho,\alpha+\theta)$. Its Cartesian coordinates are therefore given by the preceding system, where we put $\alpha+\theta$ in place of $\alpha$: \begin{align*} x' &= \rho\cos\left(\alpha + \theta\right) \\ y' &= \rho\sin\left(\alpha + \theta\right). \end{align*} applying the addition formulas of sine and cosine and also taking into account the initial formulas, we obtain the rotation formulas, in fact: \begin{align*} x' &= \rho\cos \left(\alpha+\theta\right) = \rho\left(\cos \alpha \cos \theta - \sin\alpha\sin\theta\right) = x\cos\theta-y\sin\theta, \\ y' &= \rho\sin\left(\alpha+\theta\right) =\rho\left(\sin \alpha \cos \theta + \cos \alpha\sin\theta\right) = x\sin\theta+y\cos\theta. \end{align*} Although it is simple it is necessary to remember goniometry in the third year of high school, which is not contemplated. Is there an alternative proof?
-
2Compute the images of $(1,0)$ and $(0,1)$ and extend by linearity – lhf Dec 10 '23 at 20:44
-
@lhf I have not understood. The question is for students of 16 years old. – Sebastiano Dec 10 '23 at 20:46
-
1Draw a picture of the (1, 0) and (0, 1) vectors. Under the rotation work out their new coordinates. The transformation of (x, y) is that of x(1, 0) + y(0, 1). – Paul Dec 10 '23 at 21:45
-
Your conditions are confusing. In which education system is trigonometry not expected until after the third year of high school, and how should the students understand all these trigonometric functions in your formulas if they have never had trigonometry? Why must they learn the rotation formulas in the form you show in the final two lines of equations? – David K Dec 11 '23 at 07:04
-
@DavidK The problems are addition and subtraction formulas. – Sebastiano Dec 11 '23 at 11:09
-
Yes, we see the addition and subtraction formulas and (although you have surprisingly avoided saying so explicitly) we see that you don't expect your students to know that $\cos \left(\alpha+\theta\right) = \cos \alpha \cos \theta - \sin\alpha\sin\theta$. But you have not answered any of the questions I asked. Let me make the last one more explicit: you can write $x' = \rho\cos\left(\alpha + \theta\right)$ without using any angle-sum formula. Why is that not the final answer? The earlier questions also still apply, and are not rhetorical questions. – David K Dec 11 '23 at 18:50
-
My own high school math education was an experimental program that (if my memory is correct -- this was decades ago) introduced linear algebra before trigonometry. If that were the case with your educational program (which I think unlikely) then the first comment above would be the answer. In the education my children had, my recollection (also untrustworthy) is that trigonometry came earlier in the sequence and that by age 16 they already had learned it. And it seems odd to teach what $\sin(\theta)$ means but not teach any trig identities. – David K Dec 11 '23 at 19:00
-
1In a way, the formula $x'=x\cos\theta-y\sin\theta$ and the sum formula for cosine are equivalent -- you can easily use one to show the other. So if you want to prove the formulas at the end of your question without taking angle-sum formulas as given, essentially you must prove the angle-sum formulas. Many methods are given as answers to How can I understand and prove the "sum and difference formulas" in trigonometry? If you use one of the proofs based on rotation then you don't need to write the angle-sum formulas explicitly. – David K Dec 11 '23 at 19:04
-
@DavidK The big problem with the Italian school is that children do not study at all. It's embarrassing to explain simple concepts and not understand them. Italian high school kids are at a very low level so I have a lot of difficulty even writing written tests. I teach in a scientific high school. I feel like I'm in elementary school. – Sebastiano Dec 12 '23 at 08:58
1 Answers
We define $\phi:\mathbb{R^2}\rightarrow \mathbb{R^2}$ to be the rotation about the origin (0,0) by an angle $\theta$. We first will show that this is a linear map. We note that a rotation sends a parallelogram to a parallelogram( You can check this on your own). Let $x,y\in \mathbb{R^2}$, draw the line segment between x and the origin and do the same for y. Now you have two line segments, draw another two such that this becomes a parallelogram which we call T=(0,x,y,p) with x+y=p. If we rotate x by an angle $\theta $ and y too by an angle of $\theta$, then we have rotated our parallelogram T by an angle of $\theta$, which means every point in T is rotated by an angle of $\theta $. In particular we have that p is rotated by $\theta$. It follows that $\phi(x)+\phi(y)=\phi(p)=\phi(x+y)$. So rotating x+y=p by an angle $\theta$ is the same as first rotating x by an angle of $\theta$ and than y by an angle $\theta$ so this map is additive.
In a similar fashion you can multiply x by a constant $c\in \mathbb{R}$ and then rotate it by $\theta$. This is the same as first rotating x by an angle $\theta $ and then multiplying it by c. So we have $\phi(cx)=c\phi(x)$
We just proved that $\phi$ is linear.
Now what happens if we want to rotate (1,0) and (0,1). Let's start with (1,0): (1,0) is in the unit circle, so a rotation by an angle of $\theta $ of this point will still remain on the unit circle, since a rotation is an isometry and preserves lengths. The x and y coordinate of the rotated point are than $(\cos(\theta),\sin(\theta)) $, you can verify this by drawing a triangle :
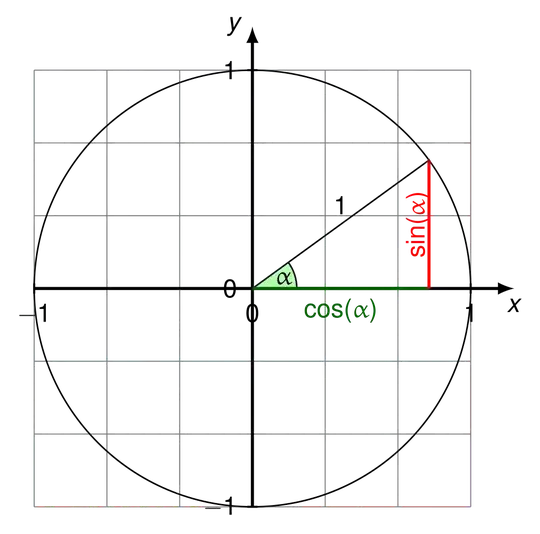
So we have $\phi((1,0))=(\cos(\theta),\sin(\theta))$
In the same way we can do this for (0,1) : Draw a circle and rotate the point (0,1) by a clockwise rotation of an angle $\theta$. After you did that try to find its respective coordinates after the rotation(you can draw a triangle again). What you will get is : $\phi((0,1))=(-\sin(\theta ),\cos(\theta))$.
You may think: Why are the images of (1,0) and (0,1) important?. Given any point (x,y) and using the fact that the map $\phi$ is linear we have the following : $$\phi((x,y))=\phi((x,0)+(0,y))=\phi(x,0)+\phi(0,y)=\phi(x\cdot1,0)+\phi(0,y\cdot1)=x\phi(1,0)+y\phi(0,1)$$$$=(x\cos(\theta),x\sin(\theta))+(-y\sin(\theta),y\cos(\theta))=(x\cos(\theta)-y\sin(\theta),x\sin(\theta)+y\cos(\theta))$$
- 258