A square of sidelength $2^n$ is divided into unit squares. One of the unit squares is deleted. Prove that the rest of the square can be tiled with $L$-trominos.
I noticed that using L trominos, we can tile $2 \times 3$ grids. Let the deleted square be a part of $2×2$ square grid, then we know we can tile the rest of the $3$ units with a single tromino. Now deleting the sqaure, we basically need to prove that the rest of the grid can be covered with $2×3$ tilings, but how do we show that?
This is a famous induction problem. It may be a duplicate.
We prove the result using induction on $n$. For $n=1$, the result is trivial, since when we remove any square from a $2\times 2$ chessboard, the remaining chessboard is itself an $L$-tromino.
Suppose that the result holds for some given $k\in\mathbb{Z}^+$, meaning that any $2^k\times 2^k$ square grid with a square removed can be tiled with $L$-trominoes. We wish to show this result for a $2^{k+1}\times 2^{k+1}$.
Lets consider a $2^{k+1}\times 2^{k+1}$ grid, with one square deleted.
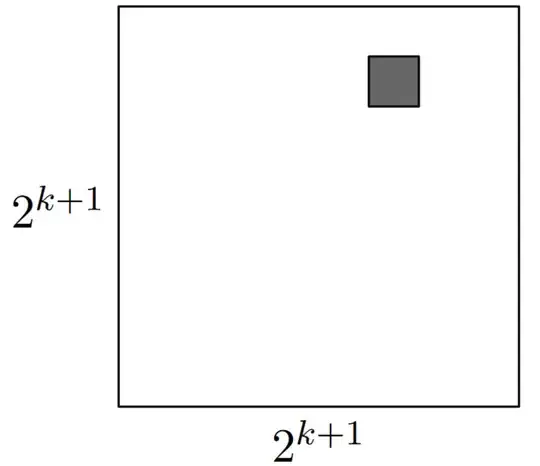
We will use the induction hypothesis. So, we can isolate the the $2^k\times 2^k$ quadrant that contains the removed square. We then can remove the middle $L$-tromino, divide the remaining grid into three $2^k × 2^k$ grids, each with a deleted square, such that the three deleted squares are adjacent to each other. As shown below;
We then have four $2^k\times 2^k$ grids with a deleted square, and by the induction hypothesis, each can be tiled with $L$-trominoes. Therefore, the whole $2^{k+1}\times 2^{k+1}$ chessboard with a deleted square can be tiled with $L$-trominoes. The result is true for $n=k+1$, and by induction, it is true for all positive integers $n$.
Hope this helps.
