According to Wikipedia :
In mathematics, a tuple is a finite sequence or ordered list of numbers or, more generally, mathematical objects, which are called the elements of the tuple. An n-tuple is a tuple of n elements, where n is a non-negative integer.
I was wondering if I can call an array of 4 numbers in C programming language a 4-tuple.
So what are the differences between array and tuple and between vector and tuple?
You ask about C language, so I will try to answer in the context of computer science.
I was wondering if I can call an array of 4 numbers in C programming language a 4-tuple.
You can call it however you want, as long as whoever you talk to understands the meaning. In that case pretty much everyone will know what you are talking about.
So what are the differences between array and tuple and between vector and tuple?
In computing an array will pretty much always mean a contiguous piece of memory. And will often hold elements of the same "size", so that we can easily refer to i-th element by doing some simple arithmetic (i*size).
The term "array" is not really well defined in maths. Some people may use this word to mean tuple or matrix. But its rather rare.
Now the term tuple is rarely used in programming. Probably only Python uses it extensively. It is actually the same as array. Since Python uses objects it sounds like tuple can keep different objects inside. But technically it holds pointers to objects, which are always of fixed size. With that any array, in any language can hold different objects.
On the other hand term "tuple" has a well defined meaning in maths: an ordered sequence or an element of Cartesian product.
Vector is a term that has different meaning depending on context. In C++ or Rust it will mean "dynamic array", i.e. array that can grow and shrink. But in C# for example it is a specialized numeric array. It's purpose is to allow compiler optimizations.
It is loosely related to maths where vector means an element of vector space, which is a structure that abstracts addition and scalar multiplication. It is not necessarily a tuple (e.g. reals are vectors over rationals) but often it is a tuple.
Here is my attempt to show the various concepts using Venn Diagram , high-lighting the various entities :
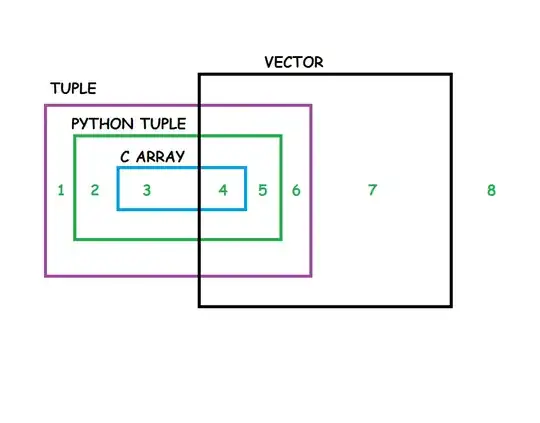
In Math , generally vectors are made of similar numbers ( Integers , rationals , reals , Complex , ETC ) which we can add & multiply. We also have Distance & Norm. There are various ways to Identify Vectors , eg $x,y,z$ Co-ordinates , Polar/Cylindrical/Spherical Co-ordinates , $\hat{i},\hat{j},\hat{k}$ ETC.
In the Venn Diagram VD , that is shown by elements 4,5,6,7.
In Math , tuples may or may not have similar numbers or entities. We can have Integer & Boolean & Set & what-not , all within a Single tuple.
That is shown by elements 1,2,3,4,5,6 in the Venn Diagram VD.
Thus , when tuple has all elements of same type which will satisfy the Criteria for vectors , we have Intersection in the VD : 4,5,6.
In C , the array can have Integers or floats or other numbers. It will then be a vector , which is also a tuple : element 4 in VD.
The array can also have Pointers or Chars or Structs. It will then not be a vector , though it is still a tuple : element 3 in VD.
In Python , the tuple can have Numbers. It will then be a vector , which is also a tuple : elements 4,5 in VD.
The tuple element numbers , which be same in C , need not be Same in Python.
The tuple elements need not be numbers in Python : Element 2 in VD.
In Math there are other Structures & Entities too , like Boolean , Number , Set , Matrix : Element 8 in VD.
1 : Math tuple $(A,B,C,1,2,3\cdots)$ : It has 3 Sets $A,B,C$ & then infinite number of elements. It is not Python tuple & not C Array & not Math vector.
2 : Python tuple $(0,\text{None},\text{""})$ : It is a Math tuple , though not C Array & not Math vector.
3 : C Array having 100 Structs : It is Python tuple & Math tuple , though not Math vector.
4 : C Array having 100 floats : It is Python tuple & Math tuple & Math vector.
5 : Python tuple $(1,2.3,0)$ : It is Python tuple & Math tuple & Math vector.
6 : Vector $(1,2,3,\cdots)$ with infinite elements : It is Math tuple too , though not Python tuple & not C Array.
7 : Vector $3\hat{i}+6\hat{j}+9\hat{k}$ : It is not Python tuple , not C Array & not Math tuple. It could be converted to the Equivalent $(3,6,9)$ which will then be Math tuple.
8 : Logical True , Integer 1 , Set $\{1,2,3\}=\{1,3,2\}=\{3,2,1\}$ , Matrix : These can be neither Math Vector nor Math tuple nor Python tuple not C Array.
Math Vector & Math tuple are very close : Every vector can have Equivalent tuple.
C Array is a type of Python tuple. Python tuple is a type of Math tuple.
There are Structures & Entities other than these.
We might have 8 types of Entities to consider.
I have given very general Examples at very high-level & certain nuances might not be covered.
When the concept of Array & tuple in Programming languages will gradually change , these Examples might have to be modified.
More-over , though there is wide consensus among Mathematicians & Programming Language Designers , it is not universal.
The Vector & Tuple might have slight variations over Country & Domain & time , which will then necessitate slight modifications to the Examples.
