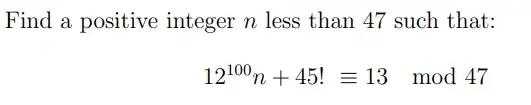The question is as follows:
So I started by attempting to calculate 12^100 mod 47 by modular exponentiation, which if I'm not mistaken, turned out to be:
12^64 * 12^16 * 12^16 * 12^4 (mod 47) = 37 * 28 * 28 * 9 (mod 47) = 34.
So the original expression becomes 34n + 45! = 13 mod 47.
Then, I attempted to work out 45! mod 47 using Wilson's Theorem:
46! = -1 mod47.
I am unsure where to go from here. Would it be correct to divide by 46 to get 45! = -1/46 mod 47?