I have seen in this link that there is a way to calculate the rolled material length and the number of turns based on:
Is there a way to calculate the length of a material roll (in my case fabric) without knowing its thickness but with knowing its number of turns?
So calculate the length by knowing:
Here is the equation you need to calculate the length $L$ of the roll approximately, when you know the number of turns $N$, the inner diameter $D_0$, and the external diameter $D_1$. We use the following two equations given in the mentioned site to derive the formula for $L$. $$L=\pi N\left(D_0+h\left(N-1\right)\right)\tag{1}$$ $$D_1=2Nh+D_0\qquad\quad\quad\tag{2}$$
From (2), we obtain an equation for $h$ in terms of $D_0$, $D_1$, and $N$. $$h=\dfrac{D_1-D_0}{2N}\tag{3}$$
Now, we substitute the value of $h$ from (3) in (1) to express $L$ in terms of $D_0$, $D_1$, and $N$. $$L=\pi N\left(D_0+\left(\dfrac{D_1-D_0}{2N}\right)\left(N-1\right)\right)=\dfrac{\pi}{2}\left(\left(N+1\right)D_0+\left(N-1\right)D_1\right)$$
In real life, various people need to know the length of material rolled around a cylinder. A simple method for doing this is to assume that the rolled material fills the volume between the inner cylinder of diameter $D_0$ and the outer cylinder of diameter $D_1$ and that neither the volume, nor the thickness, nor the width, nor the length of the rolled material changes as you roll it up or unroll it.
If $w$ is the width of the rolled material, its thickness is $h$, and its length is $L$, then the volume of the material when it is unrolled is $$V_\text{flat} = hLw. $$
But $w$ is also the height of the smallest cylinder that contains the roll, and the volume of that cylinder is $\frac\pi4 D_1^2 w$. Inside that cylinder, the volume not occupied by the rolled material is an inner cylinder of diameter $D_0$ and height $w$, whose volume is $\frac\pi4 D_0^2 w$. The volume of the rolled material is therefore the difference between these two volumes, $$ V_\text{rolled} = \frac\pi4 (D_1^2 - D_0^2) w. $$
Since (by assumption) the volume doesn't change as we roll the material, the two volumes computed above must be equal: $$ hLw = \frac\pi4 (D_1^2 - D_0^2) w. $$
So we can cancel the factor of $w$ on each side and divide both sides by $h$ to get a formula for $L$ in terms of $D_0$, $D_1$, and $h$:
$$ L = \frac{\pi (D_1^2 - D_0^2)}{4h}. $$
Not only is this a simple formula, it is actually used by people whose business it is to know what length of metal is in a rolled coil of metal.
Since we assume that the material fills the space between the inner and outer cylinder and that its thickness is still $h$ when rolled, we find that the number of layers of material, $N$, is given by $$ N = \frac{D_1 - D_0}{2h}. $$
This lets us find a relationship between $L$ and $N$:
$$ L = \frac{\pi (D_1^2 - D_0^2)}{4h} = \left(\frac{\pi (D_1 + D_0)}{2}\right)\left(\frac{D_1 - D_0}{2h}\right) = \left(\frac{\pi (D_1 + D_0)}{2}\right) N. $$
So your answer is simply $$ L = \frac\pi2 (D_0 + D_1) N. $$
Another way to write the result as describe above, if you know the inner diameter, the thickness, and the number of layers, is $$ L_1 = \pi (D_0 + N h) N. $$ (I've used the name $L_1$ for the length instead of $L$ because I'll be comparing it to other measurements of
But on the "Roll length calculator" you found, the "approximate" length is $$ L_2 = \pi (D_0 + (N - 1)h) N, $$ using $L_2$ for this estimated length to distinguish it from the estimated length $L_1$ that the other formula computes.
That is, according to that page, an approximation of the length is $$ L_2 = L_1 - \pi h N = L_1 - \frac\pi2(D_1 - D_0). $$ What accounts for this difference?
Note that the $L_2$ calculation is based on the assumption of the "Roll length calculator" that the "circumference" of the first turn of the roll is $\pi D_0$. This is a simplified model of a roll of material in which we don't worry about how the material of the first turn connects to the second turn, so all we do for the first turn is to wrap a length of the material around a cylinder until the cylinder is completely covered by exactly one layer of material. But when we do this, the material is not just a "circle" (as the "Roll length calculator" asserts) or even the surface of a cylinder, it is a cylindrical shell of thickness $h$. The circumference $\pi D_0$ is the inner circumference of that cylindrical shell, but the outer circumference is $\pi(D_0 + 2h)$.
So why does the "Roll length calculator" use the inner circumference, rather than the outer circumference, as the "length" of the first turn of the material?
Using the inner circumference, we are assuming that the side of the material next to the cylinder maintains its length, but the side of the material on the outside of the cylindrical shell stretches in order to add $2\pi h$ to its length. In this case the volume of the material gets larger when it is rolled up and smaller when it is unrolled.
If we used the outer circumference, we would be assuming that the side of the material on the outside maintains its length, but the material touching the cylinder compresses in order to reduce its length by $2\pi h$. In this case the volume of the material gets smaller when it is rolled up and larger when it is unrolled.
The assumption behind the formula for $L_1$, on the other hand, is that the volume of the material neither increases nor decreases. This means that $L_1$ is the circumference of a cylinder whose diameter is exactly halfway between the inner diameter of the cylindrical shell and the outer diameter of the shell. The circumference of this cylinder is $\pi h$ greater than the inner circumference of the shell and $\pi h$ less than the outer circumference of the shell. This means that the material on the inner surface has to compress by exactly the same amount that the material on the outer surface stretches, namely, by $\pi h$.
So according to the calculation of $L_1$, each turn of material has a length that is just $\pi h$ longer than the length assumed in the calculation of $L_2$. Since there are $N$ layers, the total "extra" length in the $L_1$ calculation (or as I view it, the missing length in the $L_2$ calculation) is $N$ times the missing length in one layer, namely, $L_1 - L_2 = \pi hN$.
If you happen to be rolling a "tape" that consists of a very thin layer of plastic with a thick layer of fibers glued to one side of it like a thick pile carpet, and you roll it with the plastic layer next to the inner cylinder, then it seems reasonable to me to assume that the inner circumference of the cylindrical shell is the same as the unrolled length of the plastic, while the fibers glued to the plastic separate slightly to form an outer surface whose length is the outer circumference of the shell. But it does not seem so reasonable to me to assume that cloth rolls this way. The $L_1$ assumption seems better.
You can force the "Roll length calculator" to compute $L_1$ instead of $L_2$ by adding $h$ to both the inner and outer diameters before computing the length of the roll. For example, suppose the roll has inner diameter $100\text{ mm}$, outer diameter $200\text{ mm}$, and thickness $0.1\text{ mm}$. Then the $L_2$ result from the calculator is as follows:
You can get the corresponding $L_1$ result as shown below by adding $0.1$ to each diameter.
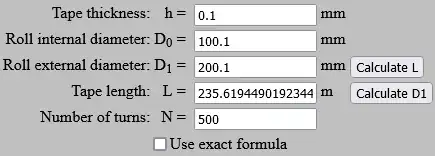
Note that the difference between these two results is $0.157079632679\text{ m}$, which is $157.079632679\text{ mm}$, which (in millimeters, to within the precision of the output of the calculator) is $\pi hN = \pi \times 0.1 \times 500$.
Now let's look at the "exact" result from the "Roll length calculator". For this calculation, it is assumed that the material is rolled into a portion of an Archimedean spiral. Let's call the resulting length $L_3$. The result for our example is shown below.
Evidently $L_3$ is larger than $L_2$, but it's not very different from $L_1$. In fact, in this example, the "exact" $L_3$ calculation gives a result that is only $0.005515890\text{ mm}$ greater than the $L_1$ result. That difference is less than $1/28000$ of the difference between $L_3$ and $L_2$.
Why is $L_3$ so close to $L_1$?
Let's acknowledge that unlike the models that gave use $L_1$ and $L_2$, in the "exact" model neither the inner turn of the spiral nor the outer turn is a cylindrical surface, so the measurement of "diameter" is already a bit suspect.
Note that if the spiral starts at radius $\rho_0 = \dfrac{D_0}{2}$ from the center of the spiral, (that is, $\rho_0 = \rho(\phi_0) = \dfrac{h}{2\pi}\phi_0$ where $\phi_0 = \dfrac{\pi D_0}{h}$, as explained in the "exact" calculation of the "Roll length calculator"), that is the only point at which the spiral touches a cylinder of diameter $D_0$ around the center of the spiral. If we imagine that this cylinder is the tube around which the material is rolled, and that the spiral represents the inner surface of the material, then the material mysteriously floats away from the surface of the tube while we roll it. So it seems wrong to say the inner diameter of the roll is only $D_0$; it should be larger.
Under these same assumptions, the outer surface of the material is always a distance $h$ farther from the center than the inner surface is. So when the spiral ends at $\rho_1 = \dfrac{D_1}{2}$, as the "exact" calculation implies it does, the outer surface ends at a point at a distance $\rho_1 + h$ from the center. If we are trying to fit the roll inside a cylinder with the same center as the spiral, that cylinder would need to have a diameter of $2(\rho_1 + h) = D_1 + 2h$, not $D_1$. It seems inappropriate to say that this is the outer diameter of the roll, since the roll would touch that cylinder at only one point. But it also seems completely inappropriate to say that the outer diameter is $D_1$, since the roll wouldn't fit in a cylinder of diameter $D_1$ at all.
Another way to look at it is that as a function of the angle $\phi$, the mean radius of the inner surface of the roll is $\dfrac{\rho_0 + (\rho_0 + h)}{2} = \dfrac{D_0 + h}{2}$ and the mean radius of the outer surface of the roll is $\dfrac{\rho_1 + (\rho_1 + h)}{2} = \dfrac{D_1 + h}{2}$, and if we use the mean radius as the radius of the "equivalent" cylinder, than the inner and outer cylinders have diameters $D_0 + h$ and $D_1 + h$. The actual diameter that you would measure would depend on how you do the measurement; for example, depending on where you put one end of the ruler on the inner surface of the roll, the other end could end up at any distance from $D_0 + \dfrac h2$ to $D_0 + \dfrac{3h}{2}$ if you measure directly across the center of the spiral.
Remember that the "exact" length $L_3$ is measured along the Archimedean spiral $\rho(\phi) = \dfrac{h}{2\pi}\phi$ from $\phi = \phi_0 = \dfrac{\pi D_0}{h}$ to $\phi = \phi_1 = \dfrac{\pi D_1}{h}$. If we use twice the mean radius of each turn as the "mean diameter" of that turn, then the first turn has mean diameter $D_0 + h$ and the last turn (the inner surface of the last layer of material) has mean diameter $D_1 - h$.
This are the diameters of the first and last cylinder of rolled material according to the assumptions used for $L_1$ when the inner diameter is $D_0$ and the outer diameter is $D_1$. So the difference between the $L_3$ result and the $L_1$ result is due to the $\frac{d\rho}{d\phi}$ term in the definition of $L_3$, which in our example is small and has a very small effect on the final result.
As a practical concern, I find it very questionable that a very flexible material such as cloth or plastic tape would form itself into an Archimedean spiral unless it were wrapped around an object whose outer surface was already in the shape of that spiral. And it seems to me that the inner surface of a roll of cloth is unlikely to have a shape anywhere near either an Archimedean spiral or a cylinder, making measurement of the inner diameter a very questionable undertaking altogether. A roll of sheet metal might conceivably take the form of an Archimedean spiral, since rolls of sheet metal are often delivered in nearly cylindrical form with nothing inside them to force them into shape.
Given that the difference between the $L_1$ and comparable $L_3$ results for a typical example is so small, questions about the assumptions (what kind of spiral does the rolled material really form, how do we measure diameter, etc.) are much more significant, and I really don't see any advantage to the so-called "exact" formula. I think a better approach is to correct the "approximate" formula by adding $h$ to the "diameter" of each layer of material, thereby obtaining the formula $$ L = \frac\pi2 (D_0 + D_1) N. $$ as derived in the first part of this answer.
