In an infinite sum, is there an actual term at an infinite position?

Question

The sum of $$ \sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n = 1, $$ exactly.

It has been proved that the sum does not just tend to 1 and that it is not just defined as 1, but rather, it is exactly 1.

How do we explain the value of n needed in order to bring the final summation to exactly 1?

(I say "final summation" because something had to add together to give a final sum of 1 exactly.)

I know "final summation" goes against current theories, and I also cannot not find a good answer to this problem without using an infinitely large n, or something else to make it make sense.

So does n have to equal infinity? If not, what is the alternative?

Answer 1

You ask, among other things, if $n$ has to equal infinity. In fact, $n$ cannot equal infinity. What $n$ does do is take on more and more values—every one of which is finite—without end. Infinity is not a number in anything like the way that 2 and 17 and 53126908 are.

You also say that “It has been proved that $n$ [here I’m sure you mean not $n$ but the infinite series] does not just tend to 1 and that it is not just defined as 1, but rather, it is exactly 1.” That is not so. One can’t prove anything about any infinite series until one has defined what “infinite series” is going to mean. What shall we mean in speaking of a sum of an unbounded number of terms?

That definition—which mathematicians have chosen—is $$\sum_{n=1}^{\infty} a_n = \lim_{N \to \infty}{\sum_{n=1}^N a_n},$$ provided that the specified limit exists. In our case, that limit does exist. Consider that when $N=3$, the sum is $$1/2+1/4+1/8 = 7/8 = 1-1/8,$$ and when $N=4$, the sum is $$1/2+1/4+1/8+1/{16} = 15/16 = 1 - 1/{16}.$$ I think you can see that in general, the sum for any $N$ is $1-1/{2^N}$. So we can guarantee that the difference between our sum and 1 is smaller than whatever positive threshold we wish, no matter how tiny, simply by adding up enough terms, in other words by choosing $N$ large enough. And that’s what we mean when we say that the limit exists and equals 1.

That argument is our basis—but it’s also our only basis—for saying that $\sum_{n=1}^\infty 2^{-n} = 1$. And it makes sense only because of how we have chosen to define infinite series, or what you might casually describe as “summing from 1 to infinity.”

Answer 2

The alternative you seek is the very definition of what that infinite sum means. There is no

value of $n$ [that] bring[s] the final summation to exactly $1$.

The infinite sum is defined to be $1$ because you can make the finite start as close to $1$ as you like if you use enough terms. In particular, you can check that the sum of the first $n$ terms is $1-1/2^n$ so when $m > n$ the sum of the first $m$ terms is within $1/2^n$ of $1$.

Answer 3

Pay attention to the summation boundaries:

$$\begin{eqnarray} \sum_{n=1}^\infty 2^{-n} &=& k \\ \frac{k}{2} &=& \frac{1}{2}\sum_{n=1}^\infty 2^{-n} \\ &=& \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots + \frac{1}{2^{\infty+1}}\\ &=& \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots + \frac{1}{2^{\infty}}\\ &=& \sum_{n=2}^\infty 2^{-n} \\ &=& \sum_{n=1}^\infty 2^{-n} - \frac{1}{2} \\ \frac{k}{2} &=& k - \frac{1}{2} \\ k &=& 1 \\ \sum_{n=1}^\infty 2^{-n} &=& 1 \end{eqnarray}$$

Supposing you wanted to do mindless addition instead of relying on the perfectly sensible algebraic solution, your error will be the size of your last included term. For example, including 2 terms, $\frac{1}{2}$ and $\frac{1}{4}$, leaves the sum $\frac{1}{4}$ away from the correct answer. Which is a roundabout way of saying that $n$ must get to infinity because if it doesn't, you have an error of $2^{-n}$.

EDIT:

Per the comments, I should definitely have proven that the series converges. There are a lot of complicated methods for that, but this picture does a good enough job. The boundary of the box is $1$ which means it has an area of $1$; it converges. As for what infinite summation means ... Zeno's first paradox maps to this very problem. Infinite summation shows how an infinite number of terms can sometimes add up to a finite number.

Edit 2:

Per a long conversation in the comments, we found that a misunderstanding about the set of natural numbers is at the heart of the confusion. The set of natural numbers, $\mathbb N$, has an infinite number of elements because for $n$ in $\mathbb N$, $n+1 = m$ defines a new natural number $m$. Despite this, $\infty$ is not usually defined to be an element of this set because we can't do arithmetic on it in the same way: $n \cdot m = l$ where $l = n$ iff $m = 1$, whereas $\infty \cdot x = \infty$ for $ x > 0$, etc... The "final" term, $\frac{1}{2^\infty}$, evaluates with a straightforward limit to $0$. In essence, the confusion stemmed from the opacity of $\infty$ within these axioms.

Answer 4

Others have tried to answer your direct question, but based on your interactions here, I believe your confusion is actually about what a limit is and how it works, so I will try to answer that instead.

A limit of a sequence of numbers $s = (s_0, s_1, s_2, ...)$, if it exists, is a number such that eventually (starting from far enough in the sequence), all elements of the sequence are arbitrarily close to $\mathsf{limit}(s)$.

To make the above a bit more mathematically precise: a number $n_{lim}$ is a limit of a sequence $s$ if and only if for an arbitrary error bound $\epsilon$, all numbers of the sequence but those from some finite inital portion of it are within the interval

$$(n_{lim} - \epsilon, n_{lim} + \epsilon)\,.$$

Notice that the limit itself needs not ever be present in the sequence itself! It is sufficient that the sequence gets "closer and closer". For example, the limit of $(0, 0.3, 0.33, 0.333, ...)$ is $1/3$, despite that $1/3$ is not an element of the sequence.

Also notice that taking the limit is not a process that computes someting / eventually spits out some number. (Even though you can intuitively think of it in such way, if you prefer.) A limit is simply a number which satisfies the above formal definition.⁰

---

Now back to

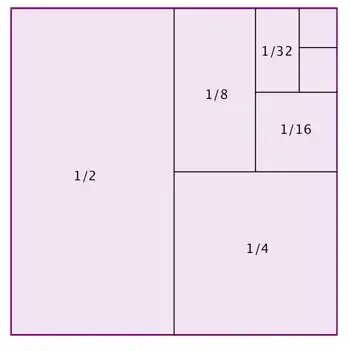
$$\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n = 1\,.$$

In math,

$$\sum_{n=1}^{\infty}\dots$$

is defined as

$$\mathsf{limit}(\sum_{n=1}^0\dots,\sum_{n=1}^1\dots,\sum_{n=1}^2\dots, \dots)\,.$$

That is, we're defining how to perform an infinite summation by trying to find out which number we're approaching as we sum more and more terms. Again, the result needs not appear at any finite "stage" of the "process", it just needs to get "closer and closer".

So we have

$$\begin{align*} \sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n &= \mathsf{limit}( \sum_{n=1}^0 0.5^n, \sum_{n=1}^1 0.5^n, \sum_{n=1}^2 0.5^n, \dots)\\ &= \mathsf{limit}(0, 0, 0.5, 0.75, 0.875, ...)\,. \end{align*}$$

Now take any arbitrary bound, let's say $0.3$. All numbers of this sequence except the initial three are within $(1-0.3, 1+0.3)$. Let's take a tighter bound, $0.2$. All but the initial four are within $(1-0.2, 1+0.2)$. In fact, we can prove that for any positive $\epsilon$, only the initial <I-don't-know-how-many> elements are going to be outside $(1-\epsilon, 1+\epsilon)$, all the rest are within. That's why

$$1 = \mathsf{limit}(0, 0, 0.5, 0.75, 0.875, ...)$$

---

Footnotes:

0. It is provable that any two numbers that are a limit of the same sequence equal each other. Therefore, any sequence has at most one limit (but may have none if it diverges).

Answer 5

Infinity can be a number in the way that 2 and 17 and 53126908 are. Namely, in the set of hypernatural numbers $\mathbb N^\ast$, an infinite hypernatural, say $H$, is precisely a number greater than every standard natural number $n\in \mathbb N$. The reason the expression $\sum_1^\infty \frac{1}{2^n}$ is taken to be exactly $1$ is because it is defined to be the standard part of the sum $\sum_1^H \frac{1}{2^n}$. Applying the standard part discards the infinitesimal part of the sum. In other words, it "rounds off" the sum to the nearest real number.

In the case at hand, applying the standard part has the effect of removing the negative infinitesimal you were puzzled about (in other words, the sum $\sum_1^H \frac{1}{2^n}$ is strictly smaller than $1$ as you expected, before the application of standard part. For details see Keisler Elementary Calculus with Infinitesimals.

The other answers talk about limits, but limit itself can be viewed as applying two operations: (1) evaluating at an infinite index $n=H$, and (2) applying standard part.

Unlike $\pi$, a hyperinteger $H$ shares all the first-order properties of the standard integers $1,2,3,\ldots$.