2

I prepare high school students for their Oxford University math interview. There is a list of $99$ interview questions that has been floating around the internet for years. Presumably these questions were posted by students after their interviews.

Many students have asked me about Question #15: "Integrate $\frac{1}{1-\ln x}$". This integral cannot be expressed in terms of elementary functions, so it is probably not suitable for high school students.

Naturally, we wonder why this question appears on the list. Maybe the original question was a definite integral, and the student who posted it thought that they had to do the indefinite integral first. (There are countless examples of integrals that can be done definitely but not indefinitely.)

So my question is:

Are there are two different real numbers $a$ and $b$, expressed in closed form, so that $\int_a^b \frac{1}{1-\ln x}\mathrm dx$ has a closed form?

My attempt

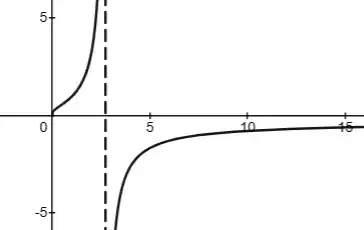
Here is the graph of $y=\frac{1}{1-\ln x}$.

enter image description here

I don't know any method other than trial and error. I've plugged into Wolfram various $(a,b)$ without success: $(0,1), (0,\frac{1}{e}), (0,\sqrt{e}), (e^2, e^3)$, etc.

Dan
  • 22,158
  • 1
    I guess it's not easy to find such numbers. I'd start with $(e, +\infty)$ and represent the integral as series. – openspace Nov 16 '23 at 10:29
  • real numbers ? I guess $\infty$ is not allowed then – pie Nov 16 '23 at 14:01
  • Expanding more on @openspace 's comment, the only way I can seem to thing about this question is to represent it as a series and give approximate solutions approaching it's asymptotes, it should look something like this, $\int\frac{1}{1-\ln x}dx = \sum_ {}\int (1-lnx)^n dx$ , I'm pretty sure this is outside the scope of an high school education though. – Amy Skinner Nov 17 '23 at 01:00
  • There are two possible explanations for the question to appear on the list. Either they expect you to express the answer in terms of some more esoteric named functions, such as $\text{Ei}(x)$, the exponential integral function. Or as an interview question, they expect you to recognize this cannot be expressed in terms of elementary functions and operations, and to be able to explain this in the interview. – Paul Sinclair Nov 17 '23 at 04:20
  • @AmySkinner firstly, it's better to start with change of variables (because Taylor for $\log (1 + x)$ is only for $|x| < 1$). Secondly, I have a doubt that high schoolers are familiar with integration in general. At least in my country, we dealt with it at the the end of the school. – openspace Nov 17 '23 at 09:07
  • Just and idea (assuming $b < e$ and $a > e^{-1}$):

    $$ \int_a^{b} \frac{1}{1 - \log x} dx = \int_{\log a}^{\log b} \frac{e^x}{1 - x} dx = \sum_{k \ge 0} \sum_{m \ge 0} \int_{\log a}^{\log b} \frac{x^{m + k}}{k!} dx $$. For symmetric parts ($e^{-1}$ and $e$ f.e.) we can notice that most of the parts eliminate.

     – openspace Nov 17 '23 at 09:26

0 Answers0